| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- GCP
- Retry
- requests
- top_k
- login crawling
- 공분산
- 상관관계
- API Gateway
- session 유지
- subdag
- youtube data
- GenericGBQException
- Counterfactual Explanations
- 유튜브 API
- integrated gradient
- airflow subdag
- gather_nd
- grad-cam
- flask
- hadoop
- XAI
- TensorFlow
- API
- UDF
- Airflow
- chatGPT
- BigQuery
- tensorflow text
- correlation
- spark udf
- Today
- Total
데이터과학 삼학년
[ISLR] Linear Model Selection and Regularization 본문
Linear Model은 일반적으로 leat square 방법을 이용해 계수를 추정하여 모델을 구했다. (OLS)
이번 장에서는 OLS 가 아닌 방법으로 linear model을 개선하는 방법을 알아본다.
OLS는
1) 오차의 평균이 0,
2) 오차의 분산이 모든 x의 단위에서 등분산,
3) 오차가 서로 uncorrelated인 경우
linear한 모델 중 최적의 모델이다.(iid일 필요도 없다! 자세한 설명은 BLUE)
오차의 분포가 정규분포일 경우, OLS estimator는 maximum likelihood estimator와 동일한 결과를 얻음
이 전까지 least square의 범용성을 보았을때 왜 least square가 아닌 방법을 사용하는 이유는!!?
몇몇 경우에, 전통적인 least square보다 더 좋은 예측 정확도와 더 좋은 해석력을 보이기 때문이다.
예측정확도 : 가정된 분포가 어느정도 맞다면, least square는 상당히 좋은 low bias의 추정을 할 것이다. 변수의 갯수 보다 총 자료수가 ‘훨씬’ 더 많다면. 그러나 n이 p보다 눈에 띄게 많지 않다면(보통 3배) least square는 훨씬 큰 변동성을 갖게 되고, 결과적으로 주어지지 않았던 새로운 자료에 대하여 예측을 잘 못하는 overfitting의 결과를 낳게 된다. 혹은 변수갯수 p가 n보다 더 많다면, 더이상 least square의 유일한 해가 없게된다. 즉, Variance가 무한이 되는, 아예 쓸 수 없는 방법이 되버린다.
해석력 : least square는 실제 Y의 함수이해에 큰 관계가 없는 변수를 없애주지 못한다. 즉, 해당 변수의 계수βi가 0이 되어야 함에도 least square가 자동으로 0을 찾기는 매우 어렵다.(그래서 앞장에서는 해당 검정들을 시행하였다.) 이번 장에서는 이런 중요한 변수를 자동으로 선택 할 수 있는 기법들을 알아본다.
왜 n<p일 경우 해를 구할 수 없다 하는 것일까?
3장에서 다항선형회귀일 경우 OLS를 통한 회귀계수의 추정을 다음과같은 matrix 연산으로 계산함을 언급했다. β^=(XTX)−1XTY 이때 X는 (n∗p)의 matrix이다. 위 식은 XTX의 inverse matrix가 존재해야 해가 나오는데, p>n인 경우 X는 모든 열(또는 행)이 선형독립이 아닌, 즉 full rank가 아닌 matrix이다. (참고) 따라서 XTX역시 full rank가 아니고, 이는 비가역행렬, 즉 위 식을 풀 수가 없게됨을 의미한다. (rank(XTX)=rank(X))
추가로, OLS의 가정이 맞고, 실제 모회귀선이 linear일 경우, bias=0이고 variance=p∗σ2n이다. 즉, 변수 p가 늘어날 수록 모델의 variance가 커진다. 참고
이를 해결하기 위한 많은 방법이 있으나 여기서는 가장 대표적인 3가지를 다룬다
Subset selection : 앞장에도 나왔던 방법. 유의미한 변수들을 골라내고, 이에 대해 least square를 하는 방법.(경우의 수 :2^p)
Shrinkage : p개의 모든 변수들로 정합을 한다. 그러나, 이 때의 계수들은 least square에 비하여 더욱 0으로 가고자 하는 경향이 있다. 어떤 shrinkage의 방법을 쓰냐에 따라 다르지만, 어떤 방법들은 정확하게 0으로 추정하기도 하여, 자동적인 변수 선택을 가능하게 한다. regularization이라고도 한다.
Dimension Reduction : 큰차원(p차원)의 p개의 예측변수를 M차원으로 projection시키는 것이다. 이를 통해 M개의 linear combination이 나오고, 이를 M개의 예측변수로써 사용하여 least square를 하는 것이다.
앞으로의 예시는 회귀에 중점을 두고 있지만, 4장의 classification과 같은 다른 방법에도 적용될 수 있다.
Subset selection
Best Subset Selection -> 경우의 수 : 2^n
best subset selection은, 가능한 모든 경우의 수의 적합을 해보고 이 중 best 를 찾는 것이다. 다음의 알고리즘을 사용한다.
모든 사이즈에 대해 최적의 적합을 찾아낸다. 즉, 다음과 같다.
변수k개만 포함한 모든 모델을 적합한다.
그 중 가장 좋은 모델을 하나 뽑는다. 변수의 갯수가 같으니, 비교는 단순히 R2으로 해도 된다.
그렇게 뽑힌 각 변수사이즈 내에서의 best model중, 최고의 single best model을 뽑는다. 이때는 평가 기준은 변수의 갯수가 다르니 R2를 사용하지 못하고, CV-error, Cp, AIC, BIC, Radj이 될 수 있다.
2번에서 R2를 사용하지 않는 이유는 간단하다. 높은 R2는 low training error를 의미하는 것으로, 변수가 많아질 때마다 그를 토대로 한 training set에 대한 설명력은 높아질수 밖에 없다.(3장 참고)
(--> 변수가 증가할 수록 low training error 자체는 작아진다는 것을 의미)
그러나 우리의 목표는 low test error이므로, 다른 지표를 사용하는 것이다. 다른 지표에 대한 설명은 잠시 뒤에 나온다. 추가로, 위에선 least square의 경우로써 R2를 사용하였지만 로지스틱회귀 같은 경우 deviance로써 계산한다.
deviance는 sum of square의 generalized 버젼으로, maximum likelihood로 적합한 모델의 goodness of fit을 측정하기 위한 척도로 많이 사용된다. 참고 saturated model과 Reduced model 에 대한 likelihood ratio test에 대한 지표로 보면 된다.
그러나 이는 2^p개(넣냐 안넣느냐)의 모든 가능한모델을 적합해야 함을 의미하므로, 예상했겠지만 computation 적으로 매우 힘들다. 심지어 요즘의 computation으로도 p가 40개가 넘어가면 힘들기에, 실질적으론 다음의 방법이 더 많이 사용된다.

Stepwise selection -> 경우의 수 : n!
계산적 문제 외에도, best subset selection은 여러 모델을 반환해준다는 점에서 p가 커지면 잘못된(overfitting된) 모델을 고르게 될 확률이 커진다는 단점이 있다고 할 수 있다. 따라서 그 대안으로는 stepwise 방법이 사용된다
이는 3장에서도 소개하였듯이, 다음과 같다. 여기에서는 추가적인 사실만을 덧붙여 제공한다.
전진 선택법 :
1)아무 변수도 포함되지 않은 모델에서
2) t통계량이 제일 유의한 변수 한개를 넣는다( 기준은? 한 변수에 관해서는 F통계량, t통계량, 오차 제곱합 감소 다 같은 결과를 낸다, 암꺼나로 해도 됨)
3)해당 변수를 넣은 상태에서 2번을 계산하여 또 하나를 넣는다. (변수 하나가 기본으로 들어가 있으니 p-value가 달라짐)
4) 더이상 중요한 변수가 없으면(t 통계량이 유의한게 없으면) 멈춘다
이 경우 변수p가 20개 였다면, best subset 은 1,048,576번의 적합을 해야하지만 전진선택법은 211번의 적합만을 하면 된다. 그러나 한 변수만을 고려했을땐 X1이 제일 잘 설명하지만 2변수를 고려했을땐 X2,X3이 더 잘할 수 있기에, 꼭 best 모델을 찾게 되는것은 아니다. 둘이 합쳐짐으로써 낼 수 있는 설명이 기존의 X1이 들어간 변수2개짜리 모델, 즉 X1, X2나 X1, X3보다 잘할 수 있다. 그리고 n<p인 경우 처음에는 적합을 할 수 있지만, high dimension단계, 즉 적합하려하는 변수갯수가 전체 데이터n보다 많아지는 단계(n<k)에 들어서면 역시나 각 모델의 유일한 least square 계수를 찾을수 없게 된다.
후진 제거법 :
1) 모든 변수가 있는 모델에서
2) 제일 큰 p-value를 가진 변수를 지움
3) 남은 p-1개 변수로 또 p-value계산해서 뺀다
4) 더이상 뺄 변수가 없으면 멈춘다
이 역시 전진선택법 처럼 best 모델을 찾는것이 보장되지는 않는다. 주로 전진선택법은 보수적인 모델(변수가 덜들어간), 후진제거법은 변수가 많이 들어간 모델을 최종적으로 선택하게 된다. 또한, n<p인 경우, 모든 변수가 들어간 모델 자체를 적합할 수 없다는 점에서 전진선택과 차이가 있다.
전진 단계적 회귀(mixed selection)
1) 아무 변수도 포함되지 않은 모델에서
2) t통계량이 제일 유의한 변수 한개를 넣는다
3) 해당 변수를 넣은 상태에서 p-value를 계산해서 유의미 하지 않은 변수를 지운다 (이때 들어오기 위한 p-value임계점과 나가는 임계점을 다르게 한다. 보통 어렵게 들어오고(α=0.1α=0.1) 쉽게 뺀다(α=0.1α=0.15) )
4) 다시 중요한 순대로 새로운 변수를 넣는다.
5) 더이상 넣을 변수도, 뺄 변수도 없으면 멈춤
위의 방법이, 사실상 계산적 부담을 덜으면서 가장 best subset selection과 비슷한 모델을 찾아준다.
Choosing the Optimal Model
앞에서 변수의 수가 다른 경우 R2가 test error의 적절한 판단 기준이 될 수 없음을 언급하였다. 따라서, test error를 최소화하는 모델을 고르고자 할때, 우리는 test error를 추정해야 한다. test error를 추정하는 방법은 다음과 같다.
1) training error rate에 overfitting을 고려한 수학적인 보정을 가하여 test error를 간접적으로 추정하는것
2) training set중 몇개를 따로 빼내서 test error를 직접적으로 추정하는 방법(5장에서 다뤘음).
Cp, AIC, BIC, and Adjusted R2
training error rate에 overfitting을 고려한 수학적인 보정을 가하여 test error를 간접적으로 추정하는 방법으로는
Cp, AIC, BIC, Adjusted R2이 있다. 이를 이용하면, 변수갯수가 다른 모델들 간의 비교도 가능하게 된다.

책의 수식의 σ^2와 위의 수식의 MSE는 같은걸 지칭한다. 둘다 σ2의 추정치라는 뜻.

SSER은 reduced model(몇개만 넣은 모델)의 SSE, MSEF는 모든 변수 적합을 통해 구한 MSE, 즉 σ^2이다. 변수의 갯수 p가 수식에 들어가 변수의 갯수에 대한 조정을 해주고 있는것을 볼 수 있다. 여기에선 결과만을 제시하지만, σ^2가 σ에 대한 unbiased estimator라면, Cp역시 test MSE에 대한 unbiased estimator이다 이 기준에선 Cp가 낮은 모델이, 가장 좋은 모델이다.
위 문장에서 irreducible error혹은 모델에 포함되지 못한 분산 σ2σ2랑 test MSE랑 헷갈릴수 있는데, 이는 다른 것이다.

이고 여기서 이다. 자세한 논의는 5장의 Cross-Validation에서 다루었다.
AIC는 maximum likelihood로 적합시킨 모델에 대한 기준이지만, error ϵ에 정규가정을 하였다면 maximum likelihood와 least square는 같은 결과를 가져온다. 참고
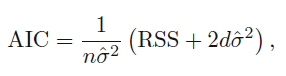
식을 보면 알 수 있지만, AIC와 Cp는 상수배이다. 즉, 사실상 같은 의미를 갖는다. 어려운 참고
BIC는 Bayesian의 관점에서 계산된 지표이다. 결과를 두고 보았을때는 AIC에서 2가 log(n)으로 바뀐 차이뿐이다. n>7이면 log(n)>2이므로 (e2는7.38정도이다) 왠만한 경우에 BIC가 더 많은 변수에 더 패널티를 주었다고 볼 수 있다.

Adjusted R2는 다음과 같다. Cp,AIC,BIC가 낮을 수록 좋은모델인 반면 adj R2는 높을 수록 좋은 모델(test error가 낮은 모델)이다.

식을 보면 알겟지만, SSE와 SST를 각각의

사실, Adj R2는 매우 널리 쓰이는 지표이지만, Cp, AIC, BIC는 많은 이론적 바탕이 있는 반면 Adj R2는 큰 통계이론적 배경은 없다.
Validation and Cross-Validation
5장에서 여러번의 resampling을 통해 test error를 직접적으로 추정해보는 validation 방법을 다루었었다. 놀랍게도 이는, 사실 위에서 다루었던 수학적 보정을 통한 Cp, AIC, BIC, adjR2 보다 이점이 많은데, 그 이유는 가정을 거의 하지 않고, 또 자유도를 구하기 힘들거나 σ^2σ^2를 구하기 힘든 여러 경우에도 사용될 수 있기 때문이다.
과거에는 computation power의 한계로 Cp,AIC,BIC,adjR2를 선호하였지만, 최근에는 cross-validation 방법이 더욱 많이 쓰이고 있다.
실제에서는, 다음과 같은 방식이 사용된다. 어떠한 회귀 문제에서, 몇개의 변수를 사용하여 적합할지를 BIC, 4-fold CV, 10-fold CV로 본것이다.

각각 변수 4개, 6개, 6개를 최적이라고 보았으나, 모든 경우에서 변수 3개까지는 추정된 test error가 급감하였으나 그 후는 크게 변동이 없는 것으로 보인다. 또한, 몇개의 그룹으로 잘랐는지, 혹은 어떻게 기존의 data가 잘렸는지에 따라서 약간씩 변동할 위험도 있다. 즉, 변수6개가 최적의 모델이 아닐 수도 있는 것이다. 이를 해결하기 위해 one-standard-error rule을 적용한다. 추정된 test MSE의 표준편차 standard-error를 구한뒤(sample mean으로 test MSE를 추정하였듯이 표준편차도 구할 수 있다 참고18쪽), 최소 test MSE추정값(예시에선 각각 4,6,6)에서 (1 X standard error) 만큼 떨어진 모델들을 모두 고려하는 것이다. 이는, 추정된 test MSE가 크게 다르지 않은 수준 내에서, 가장 단순한 모델을 고르고자 하는 목적이 있다. 이러한 방법을 사용할 경우, 변수 3개를 택하는 결과가 나오게 된다.
one-standard-error rule에서 standard error를 구하는 식은 다음과 같다.

각각 ‘1번째 fold를 빼고 적합한 모델의 CVerror’,..,’k번째 fold를 빼고 적합한 모델의 CVerror’를 의미한다. 단순히 k-fold를 통해 얻은 k개의 자료로 sd를 구했다고 받아들이면 된다.
Shrinkage Methods
위에서는 변수를 선택하고 선택된 변수로 least square적합을 하는 방법을 다루었다. 이번에는, 모든 변수로 적합을 하되 계수들을 0으로 constrain, 혹은 regularize하는 shrinkage 방법을 다룰 것이다. 이러한 방법은, 추정된 계수들의 변동(variance)을 대폭 줄여준다는 강점이 있다.
Ridge Regression
3장에서 배웠던 least square는, 다음의 식을 최소화하는 방식으로 계수를 추정하였다.

Ridge는 RSS에 L2 놈을 더한 값을 최소화하는 Linear Model 이다.

여기서 λ(≥0)는 tuning parameter로(hyper parameter라고도 한다), 분석자가 지정한다. 기존의 RSS에서, (모든 계수의 제곱합) X (지정된 상수 λ)를 최소화 하는 식이 더 붙었다. 따라서 계수들이 작아지도록 유도하게 된다. 이로써 ridge regression은 RSS를 최소화함으로써 데이터에 잘 적합하는 동시에, shrinkage penalty라고 불리는

을 통하여 계수들(β1,..,βp)이 0으로 가게하려는 shrink의 효과 역시 부여하는 것이다.
머신러닝, 딥러닝에서 많이 쓰이는 L2 regularization term이 덧붙은 것이라 보면 된다. parameter의 크기가 지나치게 커지지 않도록 제한을 걸어주는것.
해당 식에서 β0은 shrink의 대상에 들어가 있지 않음에 주의해라. β0은 단순히 모든 변수의 계수가 0일때 예측변수들의 평균으로 구하는 것이기에, 이는 shrink의 대상이 아니다.
이때 두 목표중 어디에 더 치중할 것인지는 분석자가 λ를 통해 결정한다. λ가 0이면 shrinkage의 비중을 0, λ가 커질 수록 shrinkage효과에 비중을 두는 식이다. 결국 이 λ에 따라 최종적으로 추정되는 계수들도 달라지게 되므로, λ를 결정하는 것이 매우 중요하다. 이는 cross-validation을 통하여 결정하는데, 조금 뒤에 따로 설명하겠다.
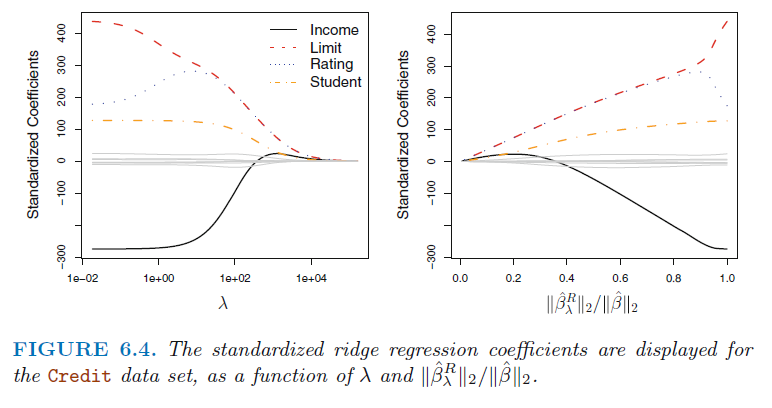
왼쪽 그림은 예시문제에서 각각의 변수(income, limit 등)들의 계수가 λ가 커져갈때 어떻게 변화하는지를 그린 그래프이다.
가장 왼쪽, 즉λ가 0일때는 기존의 least square와 같고, 점차 λ값이 커지면서 계수들이 0으로 가는것을 볼 수 있다.
그러나 Rating의 계수의 값을 보면 λ가 커질때 잠시 값이 커지기도 한다.
오른족은 같은 계수들의 값을 이번에는 x축을 λ가 아닌

이다. 분자는 Ridge regression의 계수들의 L2 norm이고, 분모는 least square의 계수들의 L2 norm이다. L2 norm은 벡터의 크기를 나타내는 방식중 하나인데, 다음과 같이 정의 된다

쉽게 다차원에서의 원점과 β의 유클리드 거리라고 생각하면 된다. 이때는 λ가 커지면 x축은 0이 될것이고, λ가 작아지면 x축은 1에 가까워 질 것이다.
X들의 표준화
기존의 least square에서, 변수의 단위를 c배 조정해주는것(예를 들어 ‘10000’만원 단위였던 것을 ‘1’억원으로 바꾸는것)은 해당 변수의 계수를 1/c만큼 조정하는 효과였다. (변수가 한단위 증가할때 ‘12345’만원 증가하는거나 ‘1.2345’억원 증가하는걸 의미한다.)
Scaling에 관하여. scaling은 각 예측변수들의 scale이 지나치게 다른경우 계수들의 scale을 통일시켜 scale이 작은 변수들의 기여를 제대로 표현하고자(주이유), 또 큰 scale에서 오는 버림오차 등에 대한 위험을 줄이고자(부가이유) 실행한다. 또한 수학적으로는 descent 알고리즘에서 가파른 기울기를 완화시켜주는 의미를 갖는다. 또한 보통 반응변수는 scale대상이 아니다. (참고)
scaling과 centering의 의의가 잘 정리되어 있는 사이트인데, 정리하자면 모든 변수들의 mean을 0으로 만들어 절편항에 대한 의미를 부여하는 것 등의 목적으로 행하는 것이 centering이고, scale의 차이로 인한 계수해석의 어려움을 방지하고자 행하는 것이 scaling이다. 다항회귀가 아닌경우, 두가지 모두 분석 자체에 영향을 미치지 않는다. centering하는것과 scaling이 되는것을 통한 그 밖의 여러 효과가 있으니 참고하면 좋다.
추가로, scaling이 되었다고 회귀계수들을 바로 변수들의 중요성으로 보는 것은 위험한데, 이는 각 예측변수들이 서로 correlated되어 있을 경우 각 회귀계수들이 다른 예측변수들에도 영향을 받기때문이다. (참고교재 283쪽)
그러나 ridge regression은

이 수식에 들어가 있으므로, 변수 Xj의 scaling이 βj에만 영향을 미치는게 아니고, 또한 다른 변수의 scaling역시 βj에 영향을 미치게 된다. (∑기호를 통해 모두 연결되어 있다.) 즉 ridge regression에서 추정되는 계수는 λ에만 영향을 받는 것이 아니라 변수들의 scaling에도 영향을 받는 것이다. 따라서 보통 ridge regression전에 모든 변수들을 다음과 같이 표준화를 해주고 진행을 한다.

위와 표준화를 해준다는 것은 같은 scale에 있게 한다는 것과 같은 의미이다. 식을 보면 각 변수의 표준편차로 나누어 주고 있다. 따라서 모든 변수들의 표준편차가 1이 된다. 이에 따라 ridge regression이 scaling에 변동하지 않게 된다. 위의 그림은 표준화를 한 경우의 계수이다.
Ridge를 쓰는 이유
이제, ridge regression을 이해하긴 했는데, 이걸 왜쓰는 건지 아직 와닿지 않는다. 왜 이런 기법을 쓰는 것일까? 그 해답은 또 bias-variance trade-off에 있다. λ가 증가함에 따라, flexibility(복잡성)는 감소하게 되고, 결과적으로 Variance는 감소하고 bias는 증가하게 된다.

위의 그림은 λ에 따른 ridge regression의 bias(검은선)과 variance(초록선)이다. 검은 선을 보면 λ가 0일때는 bias가 0, 즉 least square의 특징인 unbiased를 잘 보여주고 있다. bias는 λ가 증가함에 따라 조금씩 올라간다. 그러나 초록선Variance를 보면, λ가 증가할때마다 더욱 큰폭으로 감소함을 볼 수 있다. λ라는 제약에 따라 계수들이 shrinkage하게 되어 변동이 크지 않은 모델이 나오는 것이다.
λ는 사실 제약으로써, β matrix의 df를 줄이게 된다. 어려운 참고
이에 따라 bias의 제곱과 variance로 이루어져 있는test MSE(분홍선)는 지속적으로 감소해서 λ가 10조금 넘는 부분에서 최소점을 찍는 것을 볼 수 있다.
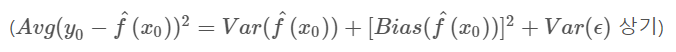
오른쪽 그림은 같은 상황을 L2 norm으로 제시한 그림이다. 역시나 bias variance의 trade-off를 확인할 수 있다.
실제 함수가 선형에 가까울때 보통의 least square방법은, unbiased하나 높은 variance를 가진 계수를 추정하게 된다. 이는 데이터가 조금만 바뀌어도 계수들이 크게 변동할 수 있음을 의미한다. 특히, p>n, 즉 설명변수가 많아질때 least square는 심지어 유일한 해가 없게 된다. 이러한 상황에서 ridge regression은 약간의 bias에서의 손해로 variance를 크게 줄여 least square보다 좋은 결과를 가져올 수 있다. 쉽게 말해 설명변수p 보다 데이터의 수n이 적을때, 더욱 덜 flexible한 적합을 하여 소수의 데이터의 특성에 국한되지 않는 모델을 만드는 것이다.
또한, 특정 λ에서의 계산은 한번만 하면 되기 때문에, ridge regression은 2p번의 계산을 해야하는 best subset selection보다 computation에서도 큰 강점을 가지고 있다.
(사실 λ에 따라서 식이 달라지는 것도 아니기에 여러 λ를 고려하는 것도 어렵지 않다.)
The Lasso
Ridge 의 단점을 굳이 꼽아보자
앞에서 다룬 Ridge regression은 특별한 단점을 가지고 있지는 않다. 그러나 변수선택법을 통해 변수를 선택하고 적합을 하는 방식과 다르게 ridge는 특정 패널티

를 통해 몇몇의 변수의 계수를 0에 가깝게 가게 만든다(물론 λ를 무한히 크게하면 다 0으로 가지만, 보통은 그렇게 안한다). 이는 예측의 측면에서는 문제가 아니지만, 해석의 측면에서 약점을 가지고 있다 할 수 있다. 예를 들어 10개의 변수중에서, X1,X3,X8이 중요한 변수임을 깨달았다 해보자. 우리는 위 3개의 변수로만 적합을 하고 싶지만, ridge regression은 그 설정상 모든 변수로 적합을 해야하고, 다른 변수의 계수는 0에 가까운 작은 값이지만(예를 들어 0.000283) 완벽한 0이 나오지는 않을 것이다.
이를 보완하기 위해 고안된 방법이 바로 Lasso이다. Lasso는 다음의 식을 최소화하는 방식으로 계수를 추정한다


식을 보면 알겠지만, ridge regression에서 최소화하려 했던 식과 매우매우 유사하다. 구체적으로 말하자면
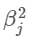
가 |βj|로 바뀌었을 뿐이다.
이를 좀더 통계적으로 말하자면, lasso는 L2 norm을 이용하여 penalty를 준 Ridge와는 달리 L1 norm을 이용하여 penalty를 준 식이다. L1역시 벡터의 크기를 나타내는 기준중 하나인데, 정확한 식은 다음과 같다.
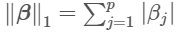
즉, 단순하게 절대값의 합을 해준 방식이다. (L2 norm은 제곱들의 합의 루트였다.) 이때도 모든 βj가 ∑으로 엮여 있기에, 같은이유로 모든 변수를 scaling해준다.
계수들이 0의 방향으로 shrink하게 했던 ridge와 달리, Lasso는 적당한 λ만으로 몇몇 계수를 정확하게 0으로 가게 만들 수 있다. 따라서 몇몇 중요하지 않은 변수가 사라진 효과이므로 해석력에서 ridge보다 강력한 강점을 가지고 있다. 물론 ridge와 마찬가지로 Lasso도 λ를 어떻게 설정할것인지가 매우 중요하다. 이는 뒤에서 cross-validation을 통해 다룬다.
전체의 변수를 포함하지 않고 몇몇 변수만을 포함한다는 의미에서, Lasso를 sparse한 model이라고도 한다.

Ridge에서와 같이 왼쪽은 λ에 따른 계수들의 값이다. λ가 0이면 기본적인 least square와 같고, λ가 커지면 계수들이 전부 0이되는 null model(아무 변수도 없는, y¯를 예측하는 모델)과 같아진다. 그러나, 오른쪽 그림을 보면 ridge와 lasso의 차이가 확연히 드러난다. 계수들이 완만하게 0으로 가며 완벽한 0이 되는 시점은 모든 계수들이 비슷한 시점이었던 위의 Ridge그림과 달리, Lasso는 Rating의 계수만 끝까지 남아있다가 0으로 사라진다. 그 전에는, Student와 Limit변수의 계수들이 남아있다가 사라졌다. 즉, λ의 수준에 따라 몇몇 변수만 0인 모델, 즉 몇몇 변수를 제외한 모델을 만들어 낼 수 있는 것이다. 이는 λ의 수준에 따라 그 크기가 shrink하긴 해도 0으로 사라지진 않던 Ridge와 구분되는 특성이다.
Another Formulation for Ridge Regression and the Lasso
L1 norm을 사용하는 Lasso와 L2 norm을 사용하는 Ridge를 여러 식으로 나타내어 다양한 방식으로 이해를 해볼 수 있다.
(위에서의 식과 아래의 식은 사실 라그랑주 승수로써 나타낸 동일한 식이다!) 다분히 수학적인 부분이지만, 아주 정리가 잘되있는 참고

이 식은 각각 특정 상수 s일때마다 위의 식들과 완벽하게 같은 결과를 의미한다. s가 무한히 크다면 사실상 제약이 없는, 즉 least square를 의미하게 되고 s가 0에 가까워 질수록 큰 제약, 즉 null model이 된다. 즉 어떠한 상수 s보다 해당 ∑들이 작은 제약 안에서, RSS를 최소화하는 것이다.
이는 변수가 2개일때,
lasso의 경우

인 사각형 공간에서 RSS를 최소화하는계수를,
ridge의 경우

의 원공간 안에서 RSS를 최소화는 계수를 찾는 기하학적인 해석을 가능하게 한다.
또한, 이러한 형태의 식은 best subset과 ridge, lasso의 관계를 밝혀주기도 하는데, best subset selection은 다음과 같이 나타낼 수 있다.
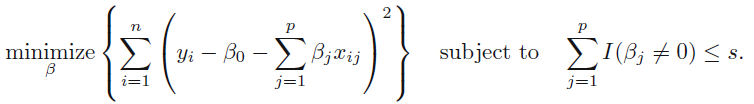
해당 식은 best subset의 의미 그대로 몇개의 βj가 0일때 RSS를 최소화하는 지점을 판단하는 것이다. 그러나 이는 best subset의 단점에서 나왔듯이 각 s마다

번의 모델을 계산해야 한다는 한계가 있었다. 이러한 점에서, lasso와 ridge는 위의 best subset selection의 식을 실현 가능한 형태로 대체한 식이라고 볼 수도 있다. 물론, lasso가 명확하게 변수를 없앤다는 점에서 best subset과는 더 유사하다.
The Variable Selection Property of the Lasso
그럼 왜? Lasso는 몇몇 계수들을 정확하게 0으로 보내는 성질을 갖는 것일까? 그에 대한 해답은 바로 위에서 했던 Lasso와 Ridge의 기하학적인 해석에서 알 수 있다.

β^는 least square의 점이고, 빨간 등고선은 같은 RSS의 선이다. 그리고 왼쪽 그림의 초록색 다이아몬드와 오른쪽 그림의 원이 각각 Lasso와 Ridge의 제약,
즉


과
이다.
각각의 방법은 해당 범위 내에서, 가능한 가장 작은 RSS를 갖는 값으로 계수를 추정한다. (s가 충분히 커서 β^의 점을 포함하게 된다면 앞에서도 나왔듯이 least square와 같은 값을 추정하게 된다.) 즉 추정된 계수는 해당 제약범위와 가장 작은 RSS등고선이 만나는 지점의 값이 될 것이다.
그림을 보면 알 수 있지만, Lasso의 제약범위는 사각형 형태라서, 한 축, 즉 다른 계수가 0인 지점에서 쉽게 교점이 생긴다. 예시에서는 β2의 축에서 교점이 생겼으므로, β1=0, 즉 X1을 제외한 모델을 의미하게된다. 반면 Ridge는 제약범위가 원의 형태라서, 한 계수가 정확히 0인, 즉 축에서 교점이 생기기가 힘들다. 이러한 성질은 차원이 높아질때도 유지된다. 변수가 3개, 즉 3차원일때는 Lasso의 제약범위는 다면체가 되고 Ridge의 제약범위는 구가 된다.
Comparing the Lasso and Ridge Regression
몇몇 변수를 아예 0으로 보내 제외시킨 다는 점에서, Lasso가 Ridge보다 해석력에서 좋다는 것은 명확해졌다. 그렇다면 예측의 정확성 측면에서는 어떨까?

왼쪽 그림은 이전에 Ridge에서 나왔던 test MSE에 대한 그림의 데이터와 같은 자료로 적합한 Lasso의 test MSE이다. 역시나 초록선은 Variance, 검은선은 bias의 제곱, 분홍선은 test MSE이다.
오른쪽의 Lasso의 성능(실선)과 Ridge의 성능(점선)을 비교한 그림을 보면, 차이가 있음을 알 수 있다. 이때, 서로 다른 정규화를 쓴 두 방법을 비교하기 위해 R2를 x축으로 두었다. 두 방법 모두 bias는 거의 비슷하지만, Ridge의 Variance가 약간더 낮아, 최종적으로 test MSE도 Ridge가 약간 더 낮음을 알 수 있다. 그러나 이 데이터는 45개의 변수가 모두 Y와 관계가 있는 데이터였다. 즉, 특정계수를 0으로 보내도록 설계된 Lasso에게 불리한 데이터의 상황이다.
그럼, Lasso에게 유리할만한 데이터, 즉 45개의 변수중 실제론 2개의 변수만이 유의한 경우는 어떨까?

역시나 예상한 대로, 이번엔 Lasso의 test MSE, 즉 실선이 더 낮은 값을 가진다. 즉, Lasso와 Ridge의 성능의 우위는 데이터의 상황에 따라 다르다. 유의미한 변수가 적을때는 Lasso가, 반대의 경우 Ridge가 더 좋은 성능을 보이는 것이다. 물론, 이를 미리 완벽하게 알 수는 없을 것이므로, 역시나 5장에서 소개되었던 cross-validation의 방법이 사용된다.
정리해보자면, Lasso 역시 Ridge처럼 약간의 bias를 희생하여 기존의 least square보다 Variance측면에서 좋은, 따라서 더욱 좋은 예측을 보이는 모델을 만들어낸다. 또한 Lasso는 계수를 0으로 보내 변수선택의 효과 역시 가져, 해석력 측면에서 강점을 가지게 된다.
또한 Ridge는 shrink할때 일정 비율로 shrink를 하고, Lasso는 shrink할때 일정 상수로 shrink를 하며, 충분히 작을 경우 0으로 줄인다.
6.2-3 Selecting the Tuning Parameter
Lasso와 Ridge에서 중요한 λ를 몇으로 설정할 것인지에 대한 문제가 남았다. 이는 언급되었듯이, Cross-validation을 통해 이루어 진다. 몇몇의 λ 값들을 선정하여, 그 값들에 대해 cross-validation을 하고 가장 작은 cross-validation error를 보인 λ를 선정한다. 최종적으로 다시 모든 데이터(CV에서는 몇개는 hold out했으니)에 대해 해당 λ로 적합을 하는 것이다.

해당 그림은 위의 예시에도 나왔던, 45개(p)의 변수 중 2개만이 유의미한 변수를 가진, (단지) 50개(n)의 자료들을 10-fold CV를 통해 Lasso 적합을 해본 것이다. 왼쪽의 점선은 최적의 cross-validation error를 낸 λ지점으로, 오른쪽의 λ에 따른 계수들을 보았을때, 회색으로 표시된 중요하지 않은 변수들을 모두 0으로 보내고 중요한 변수만이 남은 모델을 만들 수 있는 λ를 10-fold CV가 아주 잘 잡아내고 있는 것을 확인할 수 있다.
Dimension Reduction Methods
지금까지 다뤄온 방법들( 몇개의 변수만을 선택하거나, 계수들을 0으로 shrink하게 하는 방법.)은, 각기 다른 방법으로 variance를 줄이기 위한 방법들이었다. 이들은 모두 원래의 변수, X1,..,Xp를 사용한 방식이었다. 그러나 이번에는, 변수 자체를 변환하여 적합하는 방법에 대해 다뤄볼 것이다. 이러한 기법을 차원축소 방법(dimension reduction)이라 부른다.
차원 축소는 다음과 같은 방식으로 이루어 진다. 기존의 p개의 변수Xp가 아닌, 기존의 변수들의 linear combination으로 만들어진 M개의 새로운 변수Zm를 만들어 낸다. (M<p이다.)

예를 들면 Z1=0.7X1+0∗X2+...+2.4Xp와 같은 형태로 기존의 p개보다 적은 M개의 변수들을 만들어 내는 것이다. 그리곤 이 ‘M개의 변수로’, 기존에 했던것 그대로 least square를 이용한 적합을 한다.

이를 통해 기존에 p+1개의 계수들을 추정해야 했던 문제가 M+1개의 계수를 추정하는 문제로 바뀐 것이다. 만약, 올바른 Zm들, 즉 올바른 선형결합을 만드는 ϕjm들이 만들어 졌다면, 이는 기존의 least square보다 더 좋은 성과를 낼 수도 있다.
그럼 ϕjm에 대해 알아보기 위해, 우선 다음의 식을 봐보자. 변수 변환 후의 적합된 결과, 즉 θmzim들의 합은 정의를 통한 약간의 변형을 통해 다음의 식으로 다시 표현할 수 있다.

잘보이게 노랑색으로 미리 표시하였는데, 마지막 2개의 등식을 보면 다음과 같은 사실을 알 수 있다. βj=∑Mm=1θmϕjm 즉, 차원축소 방법은 계수 βj들에 위와 같은 제약이 있는 기존의 적합의 특별한 케이스 인것이다.
yi=β0+β1X1+...+βpXp
=β0+(∑Mm=1θmϕ1m)X1+..+(∑Mm=1θmϕpm)Xp
이미 여러번 다뤘지만, 제약이 없는 상태에서 최적의 계수를 정하는 것보다, 제약이 있는 상태에서 계수를 정하게 되면 약간의 bias가 생기기 마련이다. 그러나, 변수갯수p가 자료의 수n보다 많을때 M«p개의 변수로 차원을 축소하는 것은 Variance를 눈에 띄게 감소시켜 결과적으로 더 좋은 모델을 만들어 낸다. 만약 M=p이고 모든 Zm이 선형독립(모든 Zm들이 다른 변수Z−m의 선형결합으로 표현되지 못하는 것. 참고)이라면, 이는 제약이 없는것과 같고 기존의 p개 적합과 같은 결과를 낸다.
차원 축소 방법은 어떠한 줄어든 변수Zm을 만들고 거기에 적합을 한다. 그러나 Zm을 어떠한 선형결합으로 만들어 낼 것인지, 즉 ϕjm을 만들어내는 방법은 다양한 방법이 있다. 여기에선, principal components와 partial east square를 다룰 것이다.
6.3-1Principal Components Regression
Principal components analysis(줄여서 PCA)는 차원 축소의 매우 대표적인 방법이다. 이는 10장에서 더욱 상세히 나오겠지만, 여기서 간략하게 다루어 본다.
An Overview of Principal Components Analysis
PCA에서는 (n X p)의 크기를 가지고 있는 X를 줄이기 위해, 다음과 같은 방식을 사용한다. 데이터들의 변동(분산)을 가장 잘 나타낼 수 있는, first principal component direction을 찾는다.

어려워 보이지만 그림으로 보면 이해가 훨씬 쉽다. 위의 그림에서 데이터의 분산을 가장 잘 설명해주는 축은, 초록색 선이다. 초록색 선을 그은 후 각 점들을 선위에 찍어 보면(projection시켜보면) 위의 자료로 낼 수 있는 가장 큰 변동을 표현할 수 있을 것이다. (다른 선을 그으면, 찍힌 점들의 분산이 first component direction의 경우에 비해 더 적을것이다.)
다른 선으로 project를 시켰을 경우, 점들의 분산이 first component direction에 비해 적다!(왼쪽은 다른 direction, 오른쪽은 first PC)
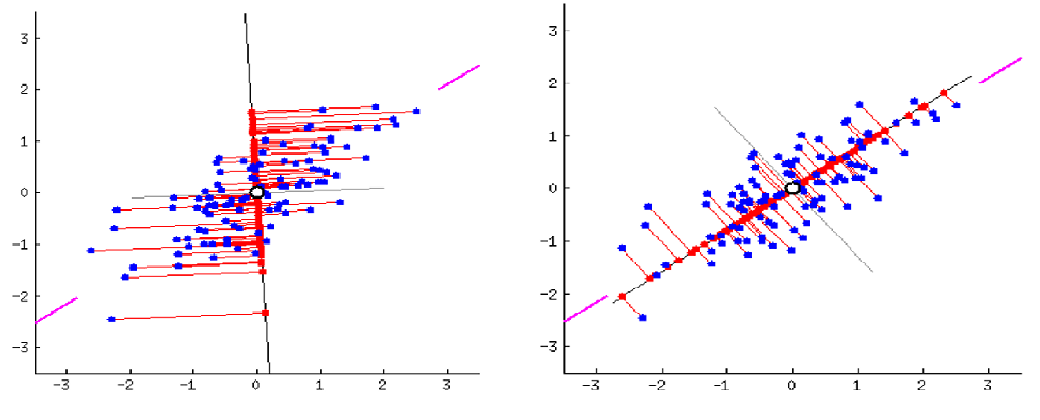
수식으로 나타내자면, 다음과 같다. (pop가 x, ad가 y이다. 이때, 데이터의 중심에 축을 두고자 변수에 centering을 하고 PCA를 진행한다. Centering은 분산에 영향을 미치지 않기에, 결과는 같다)

즉 첫번째 변수 Z1Z1을 만드는 ϕ11과 ϕ21은 각각 0.839, 0.544인 것이다. 이 수치들은 다음의 식을 maximize하는 방향으로 계산된 것이다.

이때, 계수로 인해 분산이 무한으로 커지는 것을 막고자 (ϕ211+ϕ221=1이라는 제약을 두고 maximize하는 값을 찾는다. 바꿔 말하면 ∑pj=1ϕ2j1=1이라는 제약이 있다.)
이렇게 만들어진 첫번째 변수 zi1들은 principal component score라 불리며, 다음의 그림으로 직관적으로 확인할 수 있다.

왼쪽 그림이 앞 project를 시켜주는 그림이고, 오른쪽 그림이 그 결과 만들어진 principal component scores들이다. 쉽게 축을 잡아 그 축이 x축이 되도록 회전하고 1차원으로 압축했다고 보면 된다.
또 다른, first principal component에 대한 좀더 직관적인 해석은 데이터와 가능한 가깝게 그은 선이라는 것이다. 즉, 그림에서 점선으로 표시된 수직선들의 거리가 최소가 되도록 선을 그은 것이다. 따라서, first principal component에 project된 결과는 projection중 원래의 데이터와 ‘가능한 가장 가까운’ projection 데이터이다.
오른쪽 그림에서 큰 파란점이 (pop¯,ad¯)를 의미하고, first principal component score(0.839(popi−pop¯)+0.544(adi−ad¯))는 (centering을 하였기에) 이 점과의 x축 거리, 즉 수평거리를 의미한다. 이를 통해 pop와 ad의 정보를 하나로 표현할 수 있게 되었는데, 예를 들면 zi1=−26.1이라면 pop와 ad 모두 평균(pop¯,ad¯)보다 낮은 값이고, zi1=18.7이라면 pop와 ad값이 모두 평균보다 높은 것이라고 할 수 있게 된다.
두 변수 ad와 pop가 어느정도 선형관계를 가지고 있고, 그 선형관계를 파악하여 정보를 압축하였으므로, first principal component 하나로 ad와 pop의 대부분의 정보를 포함하였다고 할 수 있다. 이는 그림을 통해서도 확인이 가능한데, ad와 pop모두 first principal component와 강한 관계를 보이고 있다.

지금까지는 첫번째 principal component만을 이야기 하였지만, 사실은 최대 p개의 다른 component를 만들 수 있다. 두번째 component, Z2는 1) Z1와 uncorrelated되어 있으면서, 2)Z1이 변수들에 대해 (많은 부분을 설명해주었지만) 미처 설명해주지 못한 부분을 설명할 수 있는 방향, 즉 Z1의 제약 하에서 가장 분산이 큰 방향으로 linear combination이 결정된다.

다시 앞의 그림에서, 아까는 설명하지 않았던 파랑 점선이 바로 second principal component이다. Z1과 Z2사이는 zero correlation이 라는 것은, 둘이 직교를 한다는 의미이다. (지금은 변수가 2개뿐이라 2개의 component가 최대지만, 더 높은 다차원에서는 직교하는 ‘여러방향’의 선들을 그을 수 있다. 그들 중 가장 variance가 높은 방향의 선을 긋는다는 의미.)
변수가 2개뿐이므로, 2개의 principal component로 인해 ‘모든 정보’를 포함하게 되었다. (평균에서 Z1방향으로 얼마나 떨어져 있는지, Z2방향으로 얼마나 떨어져 있는지) 물론, 첫번째 component에서 대부분의 정보를 포함하게 된다. 이는 Figure 6.15의 오른쪽 그림에서 2nd component score 즉 first component에서 부터의 거리를 나타내는 수치가 1st component score보다 눈에 띄게 작다는 것에서도 드러난다. 따라서 2개의 component를 모두 쓰지 않고 first component만을 쓰는, 즉 차원을 축소할 수도 있는것이다. 변수가 현재는 2개였지만, 많은 변수의 경우에도 이전의 component들에 대해 uncorrelated되어 있으면서도 variance가 가장 큰 방향으로 component를 결정할 수 있다.
The Principal Components Regression Approach
앞에서 간략하게 차원 축소 방법인 PCA에 대해 다뤄보았다. PCR은 이 PCA를 통해 만들어진 M개의 예측변수들을 통해 least square적합을 하는 것이다.
이는, ‘p개의 변수 X1,..,Xp를 가장 큰 variation으로 나타낼 수 있는 direction이 (즉 데이터의 큰 흐름이) Y와 연관이 있는 방향일 것이다.’ 라는 가정하에서 이루어 지는 분석이다. 이 가정이 항상 참이라는 보장은 없다. (전체에선 정말 지엽적인 특성이 실제 Y와의 관계에 중요한 요소였을수도 있으니) 그러나 상당히 많은 경우 좋은 적합을 보여준다. 또한, 해당 가정이 맞다면 대부분의 정보를 담고 있으나 p개만큼 많지는 않은 M개의 새로운 변수를 적합하면서 overfitting을 완화할수도 있게 된다. (n이 p보다 많이 크지 않다면 least square는 변동성이 큰 결과를 내고 overfitting에 취약해진다는것을 상기하자)

이는 위의 Lasso, Ridge의 예시에서 나왔던 예시 데이터이다. 각각 왼쪽은 45개 변수가 있고 데이터수 n은 50개이다. 이 중 왼쪽은 45개 모두가 유의미한 변수 인 데이터, 오른쪽은 45개중 2개만이 유의미한 데이터이다. X축은 component의 수, 즉 1은 first principal component만으로 적합을 한 경우를 의미한다. 45는 45개의 component로 적합을 한 경우이므로 모든 정보를 다 사용하였으니 기존의 least square와 같은 결과를 갖는다. 차원을 많이 축소할 수록 least square에 비해 bias는 커지고 variance는 줄어드는 것을 확인할 수 있다.
그림을 보면, 두 경우 모두 특정 component수에서 test MSE가 줄었지만 45개가 유의미한 경우 적당한 component에서 상당한 성능 증가를 보였다. 그러나 45개중 2개만이 유의미한 경우, 즉 전체데이터의 특성이 실제 Y와의 관계에 큰 비중을 차지하지 않는 경우 사실상 component수가 거의 45에 육박하는 것을 볼 수 있다. (사실 두 경우 모두 Ridge와 Lasso보다 test MSE가 높다.)
이를 통해 알 수 있듯이, PCR은 그 기본가정을 만족하였을때, 즉 몇몇의 component로 데이터의 variation을 잘 나타낼 수 있고, 이것이 실제 반응변수 Y와 관계가 있을때 큰 성능을 발휘한다.

이는 해당 가정을 만족하는 simulated 된 데이터이다. 왼쪽 그림을 보면, 처음 5개의 component로 데이터를 거의 완벽하게 설명할 수 있고, 따라서 5개의 component로 PCR을 하는 것이 상당한 성능의 증가를 보였다. 이는 오른쪽의 Lasso, Ridge의 적합결과 보다도 (살짝) 더 좋은 성능이다.
이전의 방법들과 주의할만한 차이점은, PCR은 변수선택법이 아니다라는 것이다. 앞의 Z1이 pop와 ad를 모두 포함한것 처럼, PCR의 M개의 변수들은 ‘모든’ 기존의 p개의 변수가 선형결합으로 포함된 변수들이다. 이러한 점에서 PCR은 Lasso보다는 Ridge와 더 관련이 있다.
사실, 수학적으로 PCR은 Ridge의 continuous version이라고도 할 수 있다.
역시나 PCR에서도, 몇개의 component를 사용할 것인지는 주로 cross-validation으로 결정한다. 또한, PCR역시, 높은 variance를 갖는 변수들이 지나치게 주요 component를 선정하는데 영향을 미치게 되므로, PCR component를 계산하기 전에 다음과 같은 식으로 scaling을 해주는 것이 좋다. (Ridge에서 나온 식. 이렇게 함으로써 모든 변수의 표준편차를 1로 만들어준 효과가 된다.)

Partial Least Squares
앞에서 다룬 PCA는, p개의 변수 X1,..,Xp의 관계를 잘 나타내는 direction을 찾는 비지도적인(unsupervised) 방법이다. 쉽게 말해 principal component를 고려하는데 Y는 쳐다보지도(supervised하지) 않았다는 의미이다. 이는 앞에서 언급되는 PCR의 단점으로 귀결되는데, 예측변수들의 관계를 가장 잘 설명하는 direction이 반응변수를 설명하는 예측변수들을 가장 잘 설명하는 direction이 아닐 수 있다는 것이다.
이러한 단점을 보완하고자 PCR의 supervised한 버젼이 partial least squares (혹은 PLS)이다. PLS는 PCR처럼 기존 변수들의 선형결합으로 M개의 새로운 변수 Z1,..,ZM을 만들어 least square 적합을 하지만, 이번엔 M개의 변수를 supervised한 방식으로 만들어 낸다. 즉, Y역시 바라봄으로 써 단순히 기존변수들의 관계를 잘 드러내는 변수를 만들어내는 것이 아니라, 반응변수와 관계된 변수들의 관계를 잘 드러내려 하는 것이다.
그럼, PLS는 어떤식으로 만들어질까? 먼저 첫번째 변수 Z1에서의 ϕj1은, 단순히 Y∼Xj의 선형적합의 계수들로써 만들어진다. 아래의 식 상기.

즉, j=1,..,p개의 변수를 각각 하나만 포함하여 Y에 적합을 한 계수들을 사용하는 것이다. Y∼Xj의 선형적합의 계수는 하나의 변수만 들어 있으므로, 사실 Y와 Xj의 상관관계(correlation)와 비례한다. 따라서 Y변수와 높은 상관관계에 있는 변수에 더 많은 가중치를 부여하게 된다.

이는 같은 데이터에 PLS를 적합한 것이다. 점선이 PCR, 초록실선이 PLS이다. 해당 데이터에서 pop가 Y와 상관관계가 더 높았기에, 기울기가 좀더 완만한, 즉 ad를 좀 덜 반영하는 direction을 찾게 되었다. 따라서 당연한 얘기지만 PLS는 PCR만큼 기존의 변수들에 잘 부합하지는 않지만, 반응변수Y를 설명하는데에는 더 뛰어나다.
2번째 변수는, 각 변수를 Z1에 적합하고 잔차(residual)을 통해 계산한다. 이는 Z1에 의해 설명되지 않은, uncorrelated (혹은 orthogonalized)data를 의미한다. 이 데이터를 가지고, Z1에서 했듯이 각각을 Y에 적합하여 계수들을 합하는 식으로 Z2를 만든다. 기본적으로 첫번째 변수가 설명하지 못한 정보를 가장 잘 설명하는 두번째 변수를 만든다는 점에서 PCR과 유사한 작동원리이다.
PCR과 마찬가지로, PLS역시 변수들을 표준화한 후 계산해야하고, 몇개의 direction을 만들것인지는 cross-validation을 통해 알아본다. 그러나 실제에선 PLS는 supervised라는 점에서 bias는 줄여주지만 그에 상응하여 variance가 높아지기에 PCR이나 Ridge만큼의 성능을 보이지 못하는 경우가 많다.
Consideration in High Dimension
High-Dimensional Data
거의 모든 전통적인 통계기법은 low-dimension, 즉 n이 p보다 훨씬 더 많은 경우를 다루고자 고안된 기법들이다. (여기서 dimension은 ‘p에 관한 dimension’을 의미한다. ) 그러나 모든것이 정보화되는 시대에, 오히려 변수가 더 많아지는 경우도 등장을 하기 마련이다. 극단적인 예로 사람의 DNA를 통한 혈압예측을 하려하면, 유의미한 변수가 몇십만개도 넘을 것이다. 이러한 high-dimension의 문제에서는 전통적인 least square가 제대로 작동하지 못하고 앞서 다루었던 방법들이 빛을 내게 된다. (물론 bias-variance trade-off의 측면에서 overfitting을 방지하고자 n>p인 경우에도 사용되기도 한다.)
What Goes Wrong in High Dimensions?
그럼, 다차원에서는 왜 기존의 통계기법들이 제대로 성능을 발휘하지 못할지를 알아보자. 여기서는 least square를 활용한 회귀문제를 다루고 있지만, 이는 다른 전통적인 통계기법, 예를들어 로지스틱 LDA등에 모두 적용되는 논의이다.
p가 n보다 많거나 비슷한 경우, least square방법은 모든 변수를 활용하여 데이터에 ‘완벽하게’ 적합한 모델, 즉 residual이 0인 모델을 만들어 버린다.

이는 변수가 1개일때의 least square 적합을 나타낸 그림이다. 직관적으로도 알수 있듯이, 모든 자료에 가능한한 적합하고자 하는 기존의 방법은 p>n일 경우 그 데이터에 완벽하게 일치하게 적합을 하고 만다.(해당 그림에선 모수의 갯수가 2인데 자료도 2개인 완벽적합이다.) 데이터를 통해 알수 없던 실재 관계를 알아보고자 하는 통계기법의 목적에서, 이는 좋지 못한 결과이다. 바꿔 말하자면 이는 완벽한 overfitting이다. 즉 p>n의 경우 기존의 least square 방법은 지나치게 flexible한 방법이 된다.
극단적인 예로 모든 X변수가 Y변수와 관계없는, 사실상 잘못된 변수들을 갖고 있다 하더라도 least square는 변수를 추가할 수록 높은 R2를 낼 것이고, 그에 따라 training MSE는 0으로 수렴하게 될것이다. 실제에서도 몇몇 유의미한 변수에 다른 의미없는 변수를 추가하는것은 bias는 (기대값의 측면에선) 아주아주 조금 낮출 수 있더라도 Variance가 커지게 되므로 지양되어야 한다.
물론 R2R2를 조정하여 test MSE를 추정하기 위한 다양한 지표, 즉 Cp,AIC,BIC등이 있지만, high dimension에서는 위의 수식에 필요한 σ^2자체를 계산하기 힘들다는 문제가 있다. σ2를 추정하는데 사용되었던 SSE가 high dimension에선 완벽적합이 되어 0이 되버리기 때문이다. (이 경우 adj R같은 경우는 1이 나오게 되버린다.) 따라서 high-dimension에서는 이를 활용하기 힘들다.
Regression in High Dimensions
high dimension에서는, 앞서 다루었던 덜 flexible한 방법들이 강점을 갖게 된다. 얼핏 예측 변수로 사용할것이 더 많은 high dimension은 더 좋은것 아닌가, 라는 생각을 할 수 있다. 물론 추가된 변수가 실제 Y와 높은 관계가 있는 변수라면 적합에 도움이 되겠지만, 추가된 변수가 반응변수Y와 실제 관계가 별로 없는 변수라면 오히려 이를 포함한 모델의 test error는 증가한다. 이러한 noise feature들은 차원은 증가시키면서도 overfitting의 위험은 높이는 작용을 하게 된다. 이렇듯 차원이 증가함으로써 생기는 분석의 어려움을 통틀어 ‘차원의 저주’라고 부른다.
Interpreting Results in High Dimensions
high dimension을 다룰때는 주의할점이 많다. 분석자는, 변수가 무수히 많으면 그만큼 correlated되 있을 가능성도 많은 것이고, 이는 분석의 안정성을 저해할 수 있다는 것을 인지해야 한다. 예를 들어 수십만개의 예측변수를 가지고 있는 DNA데이터에서 변수선택법을 통해 17개의 변수를 골라 training data를 잘 설명했다 하자. 이는, 실제로도 예측에 좋은 성능을 보일 수는 있겠지만, 17개의 변수가 DNA를 설명하는 best변수라고 말해주는 것은 아니다. train data에서는 우연히 잘 안드러 났으나 17개의 변수와 상관관계가 매우 높은 다른 변수가 실제로 DNA를 설명하기 위한 best변수 였을수도 있는 것이다.
또한, p>n의 경우 앞에서도 언급되었듯이 기존의 평가지표, 즉 R2이나 MSE를 사용하면 안된다. 별개의 test set이나 Cross validation을 통해 측정된 error를 보고하는 것이 모델의 평가지표로 의미가 있다. 이렇듯, 특히 high dimension에서는 모델의 해석에 유의하여야 한다.
[ISL] 6장 -Lasso, Ridge, PCR이해하기 · Go's BLOG
지금까지는, 회귀문제에서 다음과 같은 함수를 구하고자 하였다. 이러한 함수를 주로 ‘least square’로 구하여 적합하였다. 이는 선형모델이고, 7장(generalized linear model)과 8장에서 더욱 non-linear한
godongyoung.github.io
'Statistical Learning' 카테고리의 다른 글
| [ISLR] Tree-Based Methods (0) | 2020.03.26 |
|---|---|
| [ISLR] Moving Beyond Linearity (0) | 2020.03.19 |
| 자료포락분석(DEA), 토빗 회귀모형(절단회귀 모형 Tobit) (1) | 2020.03.04 |
| [ISLR] Resampling Methods (1) | 2020.03.03 |
| [ISLR] Classification (0) | 2020.02.18 |




