| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 공분산
- requests
- subdag
- grad-cam
- tensorflow text
- top_k
- BigQuery
- UDF
- youtube data
- GCP
- Retry
- correlation
- TensorFlow
- 유튜브 API
- Airflow
- gather_nd
- API
- login crawling
- 상관관계
- Counterfactual Explanations
- hadoop
- integrated gradient
- airflow subdag
- XAI
- GenericGBQException
- chatGPT
- API Gateway
- flask
- spark udf
- session 유지
- Today
- Total
데이터과학 삼학년
[ISLR] Resampling Methods 본문
Resampling의 기법을 이용한 학습, 예측 방법에 대해 알아본다.
Samping이란 모집단에서 모집단을 대표할 수 있는 표본을 뽑아내는 것을 말한다.
Resampling methods은 이러한 sample을 반복적으로 뽑아내고 이를 이용해 model을 학습, 예측(검증)하는 기법을 말한다.
하나의 training set에 대해 수많은 sample을 뽑아내고, 이를 모델에 적합시켰을때 각 sample로 부터 추출된 결과를 비교한다.
즉, 데이터가 달라짐에 따라 결과가 어느 범위내에 있을지에 대해 평가가 가능하다.
이 장에선 대표적인 methods인 Cross-validation과 Bootstrap에 대해 알아본다
Cross-Validation
test error VS training error
- test error는 실제로 모델이 현실 데이터에 대해 얼마나 잘 fitting 하는지를 보는 것으로 모델을 일반화할 수 있는 경향을 보는 것으로 쓸 수 있다.
- training error는 주어진 데이터에 대한 오류율로 training error을 줄이고자 모델의 compexity을 높일 경우 overfitting이 되어 실제 error을 제대로 평가하지 못하는(과소평가) 결과가 있을 수 있다.
The Validation set Approach
Validation set Approach 는 test error를 추정하기 위한 가장 간단한 방법으로 training data set을 random하게 섞은 후 split 하여 training set과 test set으로 나누는 방법이다 (반반에 가깝게 50:50).
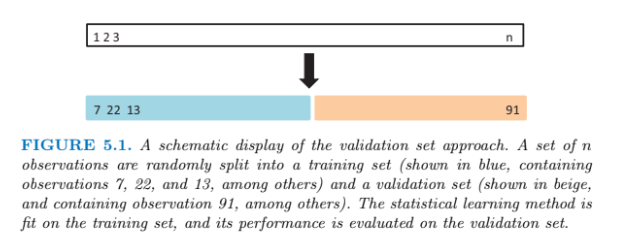
training data 에서 split되어 떨어져 나온 data set을 validation set 이라고 한다.
training set을 모델의 학습에 이용하고 validation set을 이용해 error를 구하여 전체 실제 데이터에 적용했을때 test error가 얼마나 나올지 추정하는 방법이다.
그러나 validation set approach의 단점은 data set이 어떻게 split 되었냐에 따라서 error의 추정치도 심하게 변한다는 것이다. overestimate(과대추정) 되는 단점도 있다(training dataset이 적어서).
아래 오른쪽 그림은 모델이 다차 함수(2차,3차, 4차...)로 증가할때 얼마나 error가 변하는지 측정한 것으로 2차 이후는 큰 개선이 보이지 않는 것을 알 수 있다.

Leave-One-Out Cross-Validation (LOOCV)
LOOCV의 개념은 training set에서 validation set을 split할 때 한개의 데이터 씩 빼내는 것을 말한다. 즉 training data가 100개 라면 모델은 총 100번의 학습과 예측결과를 내놓게 된다.

이 방법은 validation set approach의 단점을 줄일 수 있으나...컴퓨팅이 너무 많이 필요한 단점이 있다.
모든 자료 n에 대해 mse를 구하고 이를 평균한 값으로 test error를 추정하는 방법이다.

LOOCV는, 다음과 같은 장점이 있다.
1) 데이터의 반만을 가지고 적합을 하는 validation set approach와 달리, n-1개를 가지고 적합을 하기에 전체 training data의 test MSE에 대해 할 수 있는 거의 가장 정확한 추정을 할 수 있다. 즉, 거의 overestimate 하지 않는다. 바꿔말하면, bias가 매우 적다.
2) 어떻게 training/validation을 나누느냐에 따라 결과가 달라졌던 validation set approach에 비해, LOOCV는 n번의 모든 경우를 자르고 평균을 내기에, 결과가 달라지지 않는다.
그러나,,, 컴퓨팅이 많이 필요하다는 단점이 있다.
- Bias (fitting 정도-작을수록 overfit) : Validation Set Approach > k-Fold CV > LOOCV
- Variance (일반화 정도-작을수록 일반화 높음) : Validation Set Approach < k-Fold CV < LOOCV
K-Fold Cross-Validation
위 LOOCV의 단점을 보완하기 위한 것이 K-fold cross-validation이다. 이는 k개의 training, test set 그룹을 만들어 모델을 학습, 예측하겠다는 개념이다.

K-Fold CV의 경우, K개의 그룹에 대한 error를 평균하여 test error를 구한다.

k-fold는 LOOCV의 장점을 거의 다 가져갈 수 있다. 즉 k=n 이면 LOOCV이므로, k 그룹의 갯수를 적절히 조절하는 것이 필요하다. 적절한 k를 정하면 아래 그림처럼 각 그룹의 추정이 크게 변동하지 않는 것을 볼 수있다
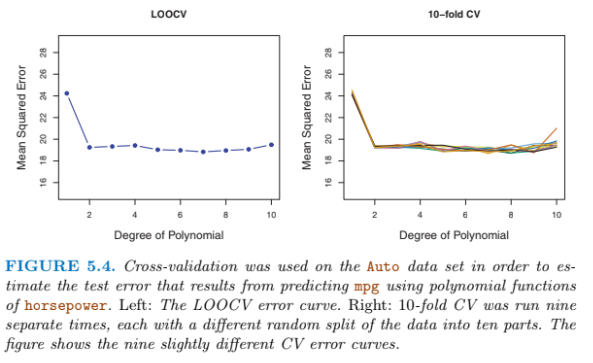
특히, k-fold는 성능면에서도 LOOCV와 큰 차이를 보이진 않는다. (bias-variance trade-off의 측면에서 LOOCV보다 강점이 있다)

Bias-Variance Trade-Off for k-Fold Cross-Validation
각 validation split 기법별 bias-variance의 trade off를 살펴보면
데이터의 절반을 잘라 사용하나는 validation set approach는 학습에 쓰이는 데이터의 양이 현저히 줄어들어 overestimate 될것이라는 문제가 있었다 (즉 bias가 높음).
이와 비교했을때 LOOCV는 거의 전체 데이터 set을 학습에 사용하기 때문에 bias는 낮고, variance가 클 수 있다.
k-fold의 경우 variance의 관점에서 LOOCV가 더 낮고, bias는 LOOCV와 거의 동일하게 가져 갈 수 있기 때문에 모델의 정확성(bias)과 일반화(variance) 측면에서 좋은 방법이라 볼 수 있다.
쉽게 말해 k-fold는 적당한 타협을 본 방안으로 볼 수 있다. k는 보통 5 or 10을 사용한다고 한다.
Cross-Validation on Classification Problems
classification 문제에서도 CV를 활용할 수 있다.

아래 그림은 차수에 따라 Classification한 정도를 나타낸 그림이다.

이를 k-fold를 활용하여 error율을 비교한 그림은 아래와 같다.
그림을 보면 k가 많을 수록 오히려 error rate이 높은 경우가 나타났다. 즉, 적당한 k를 잡는 것의 필요성을 나타내고 있으며, 이는 classification의 경우 error 산정하는 함수가 달라 나타나는 원인으로 보인다 (cross entropy or 로지스틱).

The Bootsrap
예를 들어 X, Y라는 회사에 투자비율을 각각 a, (1-a) 로 정할때, 적절한 a 값을 구하기 위해서는 X, Y의 분산을 알아야 한다. 그러나 실제 문제에서는 X,Y의 분산을 알 수 없기 때문에 복원추출을 통한 데이터 복사로 분산을 알아내기 위한 개념으로 나온 기법이다.

Bootstrap은 실제로 계산하기 어려운 추정량들의 불확실성을 계산하는데 널리 쓰이는 통계기법이다. Bootstrap은 복원추출의 개념을 이용해 학습에 필요한 data를 계속해서 생산해내는 기법이다 (분포비를 반영).
아래 그림처럼 원데이터에서 복원추출을 통해 조합을 만들어 다시 데이터로 만들어내어 모델에 학습시키는 방식이다.

아래 그림의 주황색이 원데이터이고, 청색은 원데이터를 bootstrap을 통해 (복원추출) 얻은 결과로, 추정하기 어려운 통계량의 특성까지 구할 수 있게 된다.

- 사용하는 용도 -> 추정치에 대한 분포에 대한 가정없이 리샘플링을 통해 추정치를 추정
[ISL] 5장 - Resampling Methods(CV, Bootstrap)이해하기 · Go's BLOG
재표본(Resampling)은 통계학에서 빼놓을 수 없는 요소이다. 간단히 말하자면 이는 training set에서 반복해서 sample을 뽑고, 거기에 반복해서 model을 적합시켜보는 것이다. 이는 기존의 training set 전체를 단지 한번만 쓰는것 보다 더 추가적인 정보(어떤것이든! 생각보다 많다)를 줄 수 있는데, 예를들면 다음과 같다. 하나의 training set에 대해 수많은 sample들을 뽑아보고, 거기에 각각 선형회귀적합을 해본다.
godongyoung.github.io
books : An Introduction to Statistical Learning with Applications in R
'Statistical Learning' 카테고리의 다른 글
| [ISLR] Linear Model Selection and Regularization (0) | 2020.03.11 |
|---|---|
| 자료포락분석(DEA), 토빗 회귀모형(절단회귀 모형 Tobit) (1) | 2020.03.04 |
| [ISLR] Classification (0) | 2020.02.18 |
| KL Divergence(쿨백 라이블러 발산), Jensen-Shannon divergence (0) | 2020.02.13 |
| [ISLR] Linear Regression (0) | 2020.02.10 |




