| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- youtube data
- airflow subdag
- GCP
- chatGPT
- login crawling
- UDF
- API Gateway
- XAI
- session 유지
- integrated gradient
- requests
- subdag
- API
- spark udf
- flask
- correlation
- Retry
- Counterfactual Explanations
- grad-cam
- 상관관계
- Airflow
- gather_nd
- BigQuery
- TensorFlow
- 유튜브 API
- tensorflow text
- GenericGBQException
- top_k
- 공분산
- hadoop
- Today
- Total
데이터과학 삼학년
[ISLR] Classification 본문
분류문제를 풀기 위한 기초적인 방법들에 대해 소개한다.
선형회귀로는 분류문제를 해결하기가 어렵다.
물론 Binary Classification의 경우, True or False의 식으로 값이 커질 수록 True에 가깝다는 식으로 회귀모형으로 분류문제를 풀 수도 있지만 추정된 값이 1이 넘어가는 경우 혹은 값이 음수인 경우도 발생하기 때문에 사실 좋은 방법은 아닌것으로 보인다.
물론 1,2,3을 정도의 차이를 가지는 레이블(1:보통,2:위험,3:아주위험 등)의 분류에서는 유용하게 쓸 수도 있겠다.
그러나 분류문제는 분류에 맞게 고안된 방법을 쓰는 것이 가장 좋다
Logistic Regression
선형 모형을 log를 이용해 변환한 아래와 같은 식을 사용하면 0~1사이의 확률값으로 각 레이블을 분류할 수 있다.

아래 그림은 선형회귀와 로지스틱 회귀에 대한 차이를 나타낸다.
왼쪽 그림에서 보듯이 일반 회귀모형은 음수값을 반환하는 경우도 있어 확률함수로 쓰기에 부적합함을 알 수 있다.

log-odds의 개념
로지스틱 회귀모형을 이용해 아래와 같이 식을 유추해낼 수 있다.

이때 좌변을 odds라고 부르며 이에 log를 씌운 값을 log-odds 혹은 logit이라 부른다.
logit은 X에 대해 선형관계를 가지는 식으로 볼 수 있다.
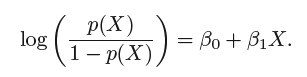

이때, 해석에 주의해야 한다. 앞장의 선형 회귀모델에서 β1은 X가 한 단위 증가할때 Y의 변화량이었지만, 여기에선 ‘로짓’의 변화량이다. 바꿔 말하면, ‘오즈’, 즉 p(X)/1−p(X)가 eβ1배 만큼 증가하는 것이다 (!!) 이때 β1이 양수면 X와 Y의 변동도 양의 관계, 음수면 변동도 음의 관계이다. (β1의 부호에 따라 함수 개형이 위아래로 뒤집힌다.)
위 로지스틱 회귀모형의 계수를 추정하기 위해서는 MLE(Maxium Likelihood)가 최대가 되게 하는 계수를 찾는다. (선형회귀의 경우 least square (OLS)를 이용하여 계수 추정)
Maxium Likelihood에 log를 씌우면 log-likelihood 라고 부르는데, 주로 log를 씌우면 곱이 합의 형태로 변환되어 연산이 쉽기 때문에 보통 log를 씌어 계수를 추정한다.
Linear Discriminant Analysis(LDA)
일차함수(직선)으로 분류하는 기법

근데 logistic regression이 있음에도 왜 다른 메소드들이 필요할까?
그 이유는 아래와 같다.

1. 이미 레이블들이 잘 분류되어 있을때 LR은 파라미터를 추정하는 것이 불안정하다.
2. 그리고 파라메터 X의 분포가 정규분포이며 표본이 작을때는 오히려 선형분류(LDA)가 LR보다 안정적이다.
3. LDA는 이진분류에 매우 적합하다.
LDA 는 Parameter가 1개 일때와 2개 이상일때 로 나누어 볼 수 있다.
1. p = 1

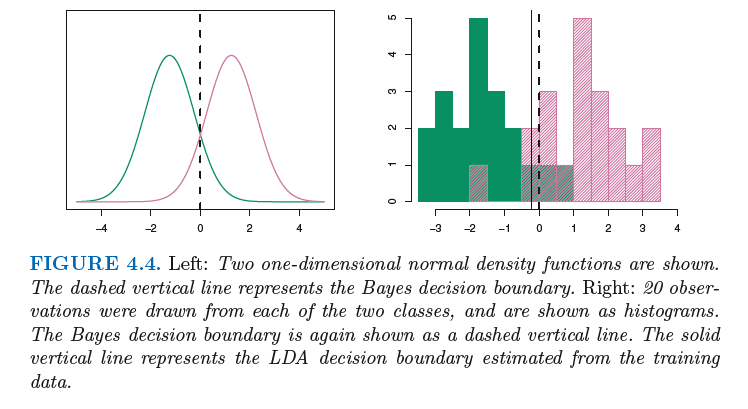
2. p >= 2

--> 사실 parameter가 2개 이상이더라도 1개일때의 식과 형태가 같다.
추정하는 식을 보면 결국 y= ax+b의 꼴로 직선형임을 알 수 있다

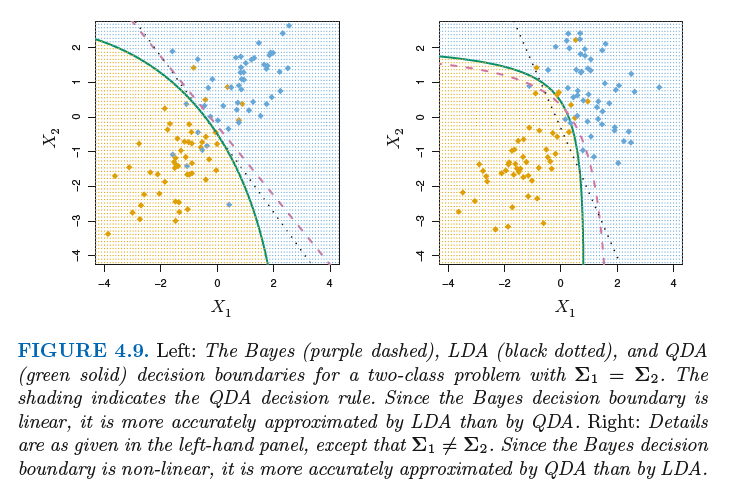
Quardratic Discriminant Analysis(QDA)
이차함수(곡선)으로 분류함
QDA는 LDA와 다르게 가정에서 모든 레이블들의 공분산이 다르다!!! 라는 가정이 있다.--> LDA의 가정을 완화

추정하는 식을 보면 결국 y= ax^2+bx+c의 꼴로 곡선형임을 알 수 있다
시나리오별 모델의 성능비교
6가지의 데이터 분포 시나리오를 나눠 각 분류 모형의 성능을 측정-비교하여 보면
시나리오 설명
1) 정규분포를 띄는 서로 다른 두 class에서 20개씩 추출
2) 1)에 사용된 feature들이 -0.5의 상관계수를 가짐
3) t-분포에서 각각 50개씩 추출
4) class 0일때는 feature들이 0.5의 상관관계, class 1에서는 -0.5의 상관관계
5) 1)이랑 같은 방법으로 만든 데이터인데, X1^2, X2^2, X1X2로 sampling됨. 즉, quadratic decision boundary를 갖는 형태로 변형됨
6) 1)이랑 같은 방법으로 만든 데이터를 뭔가 복잡한 non-linear함수들로 sampling함. 2차식으로 표현하기도 어려운 복잡한 boundary를 가짐

>> 결국 데이터의 분포별 적합한 모델은 없다. --> 정답은 없다
>> NFL(No Free Lunch) --> 다해보자!..
출처 : https://godongyoung.github.io/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D/2018/01/23/ISL-Classification_ch4.html
books : An Introduction to Statistical Learning with Applications in R
godongyoung.github.io
[ISL] 4장 - 분류(로지스틱, LDA, QDA) 이해하기 · Go's BLOG
이 장에서는 가장 많이 쓰이는 분류모델 3가지, 로지스틱 회귀, 선형 판별 분석, KNN을공부한다. 여기 안에 들어간것은 개인적인 참고를 위한 지엽적인 부분입니다. 숫자형 변수를 예측했던 3장의 회귀문제와는 다르게, 질적 변수를 예측해야 하는 경우도 있다. 질적 변수(혹은 범주형 변수)를 예측하는 문제를 classification이라 부른다. classification 방법들은 보통 각 범주에 속할 ‘확률’을 예측하는 형태로 분류를 한다. (사실 이미 여
godongyoung.github.io
'Statistical Learning' 카테고리의 다른 글
| 자료포락분석(DEA), 토빗 회귀모형(절단회귀 모형 Tobit) (1) | 2020.03.04 |
|---|---|
| [ISLR] Resampling Methods (1) | 2020.03.03 |
| KL Divergence(쿨백 라이블러 발산), Jensen-Shannon divergence (0) | 2020.02.13 |
| [ISLR] Linear Regression (0) | 2020.02.10 |
| [기초통계] t-statistic, p-value, F-statistic (1) | 2020.02.10 |




