| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- subdag
- BigQuery
- 유튜브 API
- API Gateway
- hadoop
- requests
- Counterfactual Explanations
- grad-cam
- chatGPT
- correlation
- spark udf
- UDF
- TensorFlow
- integrated gradient
- XAI
- GenericGBQException
- youtube data
- 상관관계
- top_k
- 공분산
- API
- Airflow
- session 유지
- GCP
- airflow subdag
- tensorflow text
- Retry
- flask
- login crawling
- gather_nd
- Today
- Total
데이터과학 삼학년
[ISLR] Tree-Based Methods 본문
트리 기반의 회귀, 분류 방법을 알아본다.
트리기반 방법은 설명변수를 다수의 영역으로 계층화(stratifying) 또는 분할(segmenting)하는 것이 포함된다.
주어진 관측치에 대한 예측을 위해서는 보통 예측할 관측치가 속하는 영역의 훈련데이터들의 반응변수값의 평균 또는 최빈값을 사용하여 예측한다.
이장에서는 의사결정트리, 배깅, 랜덤 포레스트, 부스팅에 대해 알아본다.
Regression Tree (회귀트리)
회귀트리는 설명변수를 공간화하여 계층화 한 후 예측치가 속하는 공간에 해당되는 관측치들의 반응변수 평균값을 이용하여 회귀값을 예측한다.
먼저 회귀트리를 빌딩하는 과정은 크게 2단계이다.
설명변수 공간생성. X1, X2, ..,Xp 에 대한 가능한 값들의 집합을 J개의 겹치지 않는 영역 R1, R2, R3,...,Rj 로 분할함
영역 Rj에 속하는 모든 관측치들에 대한 예측. 예측값은 Rj의 훈련 관측치들에 대한 반응변수값들의 평균
단계1은 아래식과 같이 RSS를 최소로 하는 R1~Rj 값을 찾는 것이 목적이다.

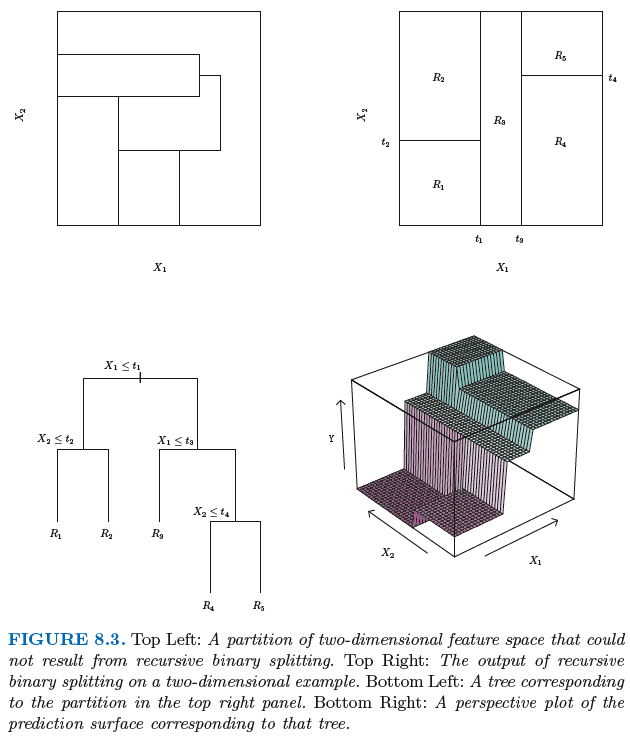
설명변수를 가지고 공간을 J개의 영역으로 분할하는 모든 가능한 CASE를 고려하는 것은 계산상 실현 불가능하다.
따라서 영역을 나누기 위해 재귀이진분할 (recursive binary splitting)으로 알려진 하향식 그리디기법을 이용한다.
먼저 재귀 이진분할을 실행하기 위해서는
설명변수 Xj와 절단점(cutpoint) s를 선택한다.
X1~Xp의 각 설명변수에 대해 절단점 s의 모든 가능한 값을 고려하고, RSS가 가장 작은 트리를 만드는 절단점을 선택한다.
상세히 말하자면
아래식과 같이 반평면(half-plane) 쌍을 정의한 후
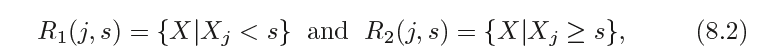
다음식을 최소로 하는 j와 s값을 찾는다.

이와 같은 방법을 반복하면서 각 영역에서 RSS가 최소가 되도록 분할한다.
이 과정은 정지기준(stopping criterion)이 만족될때까지 계속된다.
Tree pruning
위의 트리 기법은 좋은 예측을 가능하게 할 수 있지만, 데이터에 과적합(overfitting)할 가능성이 높아 성능이 나빠질 것이다.
Tree pruning은 아주 큰 tree 만들고 prune 하여 서브트리를 얻는 것이다.
LASSO 와 비슷하게 제약조건 두면 서브트리들의 전체 시퀀스를 고려할 수 있다.
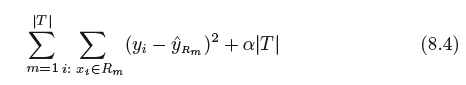
pruning의 알고리즘은 아래와 같다.
재귀 이진분할을 사용하여 큰 트리를 만든다
pruning을 적용하여 일련의 가장 좋은 서브트리들을 a의 함수로 얻는다
k-fold cross validation을 사용하여 a를 선택한다. 훈련 데이터는 k개의 fold로 나눈다
훈련자료의 k번째 fold 이외의 모든 fold에 대해 step1,step2를 반복한다
남겨진 k번째 자료를 가지고 rss를 a의 함수로 평가한다.
선택되 a의 값에 대응하는 서브트리를 선택한다.
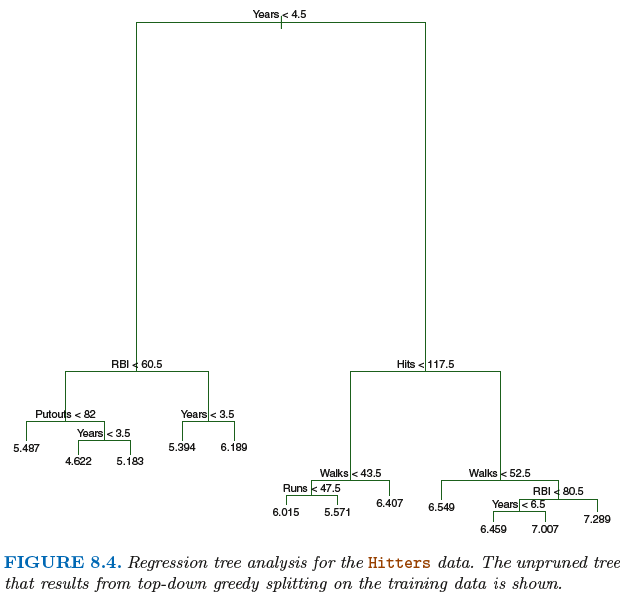
아래 그림은 pruning을 통해 얻는 결과 그림이다.
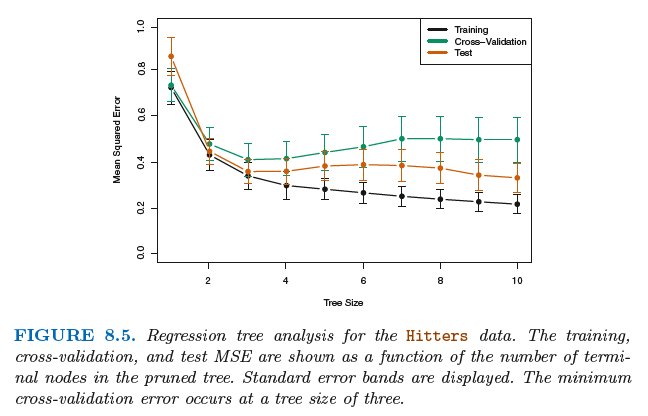
Classification Tree (분류트리)
분류트리 역시 회귀트리와 매우 유사하다.
분류의 경우에도 재귀이진분할을 사용하여 분류트리를 만든다.
다만 분류에서는 회귀에서 이진분할의 기준으로 사용하였던 RSS를 사용할 수 없다.
분류문제는 클래스를 나타내는 것이기 때문이다.
RSS에 대한 대안은 분류오류율이다.
뷴류오류율은 주어진 영역 내의 관측치 중 그 영역내 가장 많은 비율을 가지고 있는 클래스에 대해 예측치를 할당할때 나타내는 오류율을 의미한다.
분류오류율은 아래식으로 구할 수 있다.

하지만, 분류오류는 트리 빌딩에 대해 민감하지 않아서, 실제로는 지니지수(gini index)와 교차 엔트로피(cross-entropy)를 이용하여 분할의 척도를 세운다.
지니지수
Pmk ^값이 0 또는 1에 가까우면 지니 지수는 작은 값을 가진다. 지니 지수는 노드 순도(purity)라고도 불린다

교차엔트로피
교차 엔트로피 역시 Pmk ^값이 0 또는 1이면 거의 0에 수렴하게 된다.
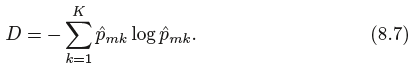

트리와 선형모델 비교
데이터가 선형모델에 잘 근사된다면 선형회귀가 잘 동작하겠지만, 설명변수와 반응변수 사이의 관계가 상당히 비선형적이고 복잡하다면 의사결정트리가 고전방법보다 나을 수 있다.
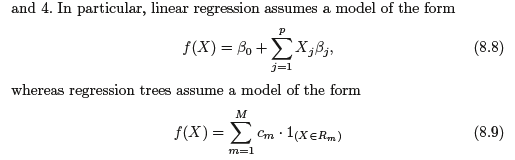
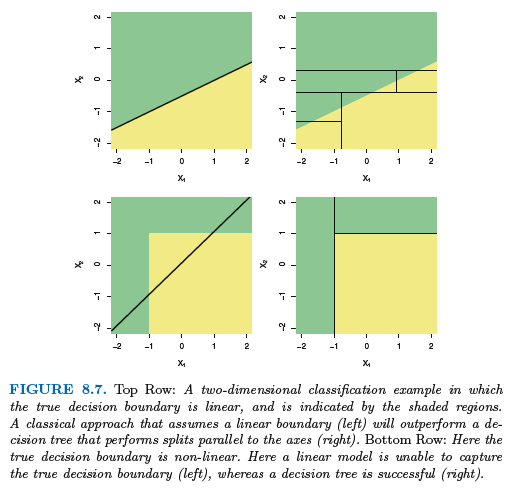
의사결정트리의 장단점
설명하기가 매우 쉽다
인간의 의사결정 과정을 더 밀접하게 반영한 모델이다
시각화와 비전문가도 쉽게 이해할 수 있다
예측 정확도가 타 모델에 비해 낮다
Bagging (배깅) - Bootstrap Aggregating
Bagging은 bootstrap 방식을 적용한 것이라고 볼 수 있다. 즉, 여러개의 tree를 만들고, bootstrap방식으로 복원추출한 데이터를 반복해 트리에 태우면서 다수의 트리가 나타낸 결과를 종합적으로 판단(평균)하는 과정이라고 보면 된다.
분산이 각각 시그마제곱승인 n개의 관측치 Z1~Zn의 집합이 주어진 경우, 평균Z의 분산은 시그마제곱승을 n으로 나눈 값으로 주어진다. 즉 관측치들의 집합을 평균하는 것은 전체적인 분산을 줄일 수 있다.
따라서 분산을 줄여 통계학습방법의 예측 정확도를 증가시키는 방법은 모집단에서 많은 수의 학습데이터셋을 취하고 각 학습 데이터셋을 사용하여 각 모델에서 도출된 결과를 평균하는 것이다.
즉, 아래식과 같이 나타낼 수 있다.
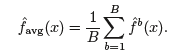
일반적인 경우에 다수의 학습데이터 셋을 가질수 없지만, 복원추출을 통한 데이터를 샘플링하면서 다수의 학습데이터셋을 만들어 적용할 수 있다는 개념이 바로 부트스트랩이었다.
bagging도 이와 마찬가지로 여러개의 데이터 셋, 여러개의 tree를 만들어 그 결과들을 평균하여 다음식과 같이 얻을 수 있다.

배깅을 회귀 트리에 적용하여 수백, 수천개의 트리들을 결합하여 상당한 정확도 향상을 이룰수 있다는 것이 연구로 입증되었다.
그렇다면 Tree가 회귀문제가 아니라 분류문제에서는 bagging 어떻게 쓸수 있을까?
각 트리에서 나온 예측 클라스를 다수결(majority vote)를 하여 가장 많이 발생된 class를 선택하는 것이다.
아래 그림은 배깅 트리의 결과를 나타낸다.
Out-of-Bag error estimation
일반 머신러닝과 달리 특별히 validation set을 나눌 필요가 없다. 왜냐면 tree는 평균적으로 전체 데이터의 약 2/3 정도를 이용한다. 즉 tree에 할당되지않은 1/3의 데이터가 있는데 이를 OOB(Out-of-Bag) 데이터라고 부른다.
트리의 갯수가 충분히 많을 경우, OOB 오차는 OOB 데이터를 Tree에 태워 측정하면 되며, 사실상 LOOCV(Leave-one-out cross-validation)의 오차와 동일하다.
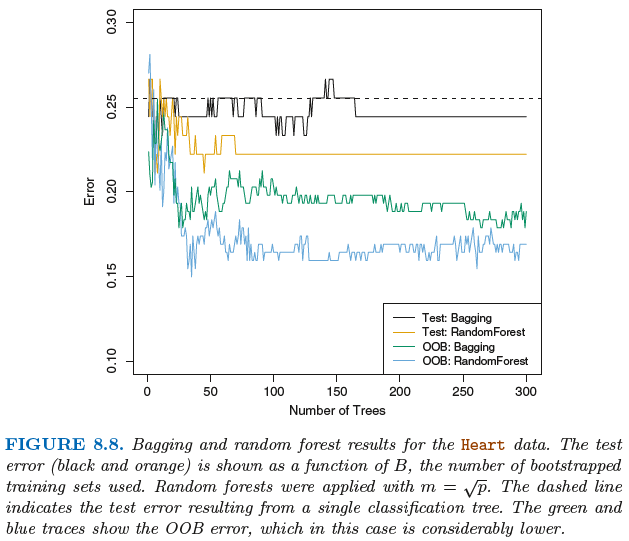
배깅은 예측정확도는 향상시키지만 tree가 여러개이기 때문에 오히려 해석은 어렵다.
Random Forest (랜덤 포레스트)
랜덤 포레스트는 트리들의 상관성을 제거하는 방법으로 배깅된 트리보다 더 나은 성능을 보인다.
트리내에서 분할이 고려될때마다 p개 설명 변수들의 전체 집합에서 m개 설명변수들로 구성된 랜덤표본이 분할 후보로 고려된다.
쉽게 말하면 bagging에서는 tree1, tree2, tree3에서 공통적으로 A라는 변수가 할당되어 비슷한 형태의 트리가 생성되었다면, 랜덤 포레스트에서는 각 변수선택 자체를 랜덤하게 제한하여 주어서 트리가 전혀 다르게 만들어지는 것을 말한다.

일반적으로 선택되는 설명변수 개수는 전체 파라미터에 루트를 씌운 값만큼 랜덤 추출된다.

Boosting (부스팅)
부스팅은 트리들이 순차적으로 만들어진다고 보면된다.
단 부스팅은 부트스트랩을 하지 않는다. 대신에 각 트리는 상위 버전의 트리에서 수정된 버전의 데이터로 적합한다.
부스팅이 되는 알고리즘은 초기 함수를 0으로 설정한 이후에, 각 만들어 놓은 트리를 순차적으로 피팅 시킨다.
이 후 순차적으로 input 데이터가 바뀌며 오차가 계산되는 방식이다.
(배깅과 유사하지만, 붓스트랩 표본을 구성하는 재표본 과정에서
분류가 잘못된 데이터에 더 큰 가중치/확률을 부여하여 표본을 추출)

아래그림은 bagging 과 boosting의 차이를 도식화한 그림이다.
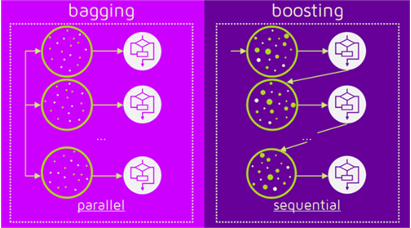

출처 : An Introduction to Statistical Learning in R
'Statistical Learning' 카테고리의 다른 글
| [ISLR] Support Vector Machines (0) | 2020.04.02 |
|---|---|
| [기초통계] 왜도(Skewness)와 첨도(Kurtosis) (1) | 2020.03.28 |
| [ISLR] Moving Beyond Linearity (0) | 2020.03.19 |
| [ISLR] Linear Model Selection and Regularization (0) | 2020.03.11 |
| 자료포락분석(DEA), 토빗 회귀모형(절단회귀 모형 Tobit) (1) | 2020.03.04 |




