| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 유튜브 API
- TensorFlow
- requests
- youtube data
- XAI
- GenericGBQException
- API
- UDF
- Retry
- Airflow
- chatGPT
- top_k
- GCP
- airflow subdag
- BigQuery
- flask
- integrated gradient
- session 유지
- Counterfactual Explanations
- spark udf
- 공분산
- login crawling
- tensorflow text
- gather_nd
- correlation
- 상관관계
- grad-cam
- subdag
- hadoop
- API Gateway
- Today
- Total
데이터과학 삼학년
[ISLR] Support Vector Machines 본문
Support Vector Machine(SVM)은 분류문제를 푸는 최상의 분류기 중 하나로 간주되어 왔다.
서포트 벡터 머신은 Maximal margin classifier (최대 마진 분류기)를 확장하고 일반화한 방법이라고 볼 수 있다.
이 장에서는
최대 마진 분류기, 이를 확장한 서포트 벡터 classifier 그리고, 비선형을 수용하는 서포트벡터 머신에 대해 알아본다
Maximal margin classifier (최대 마진 분류기)
maximal margin classifier는 hyperplane 을 정의하고, 이를 토대로 hyperplane으로 부터 일정 간격(margin) 텀을 둔 상태로 class를 분류하는 방법을 말한다.
얼핏 보면 LDA 와 유사한 개념이지만 margin을 두어 variance(일반화 측면)와 bias(정확도 측면)를 컨트롤하는 방식이다.
Hyperplane
hyperplane은 p차원 공간이 있을때 p-1차원의 affine 부분 공간을 말한다. 즉 2차원에서는 1차원이 초평면(hyperplane)이 되는 것이다. 즉 3차원의 경우, 2차원인 면이 초평면이고, 2차원인 면에서는 1차원인 선이 초평면이 된다.
2차원(X1,X2)에서 초평면은 아래 식과 같다.
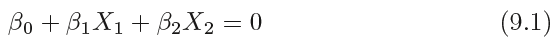
p-dimensional(차원)에서 hyperplane은 p-1차원의 공간이 된다.

여기서 hyperplane을 기준으로 hyperplane이 0이상인지 이하인지를 이용하여 클래스를 구분할 수 있다.

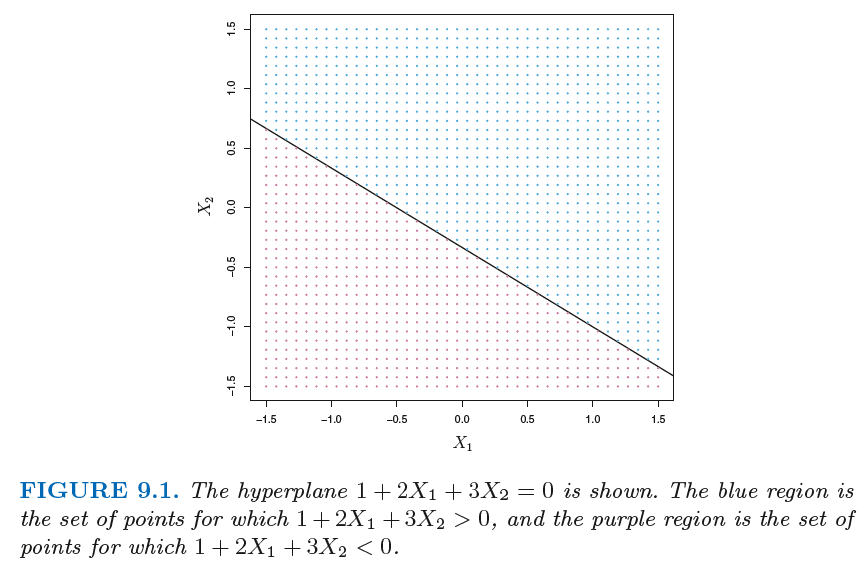
Separating Hyperplane (분리 초평면)
분리 초평면은 아래식과 같이 n개의 데이터로부터 초평면은 아래와 같이 여러개를 만들 수 있다.

위 n개의 데이터의 레이블이 파랑이면 1, 보라색이면 -1의 값을 갖는다고 하면 여러개의 초평면으로 부터 아래 그림과 같이 결정 경계를 나눌 수 있다.

이렇게 초평면을 이용하여 분류하는 기법이 separating hyperplane이다.
Maximal margin classifer (최대 마진 분류기)
최대 마진 분류기는 hyperplane을 구하고 이 초평면으로 부터 일정 간격(margin)을 만들 수 있다. margin은 hyperplane과 각각의 훈련 데이터간 수직거리를 의미한다.
최적마진 hyperplane은 이 훈련데이터에 대해 가장 큰 마진을 가지는 분류기를 의미한다.
즉 결정한 hyperplane이 근접한 훈련데이터에 대해 큰 마진을 가질 수록 분류기의 성능이 높음을 말할 수 있다.
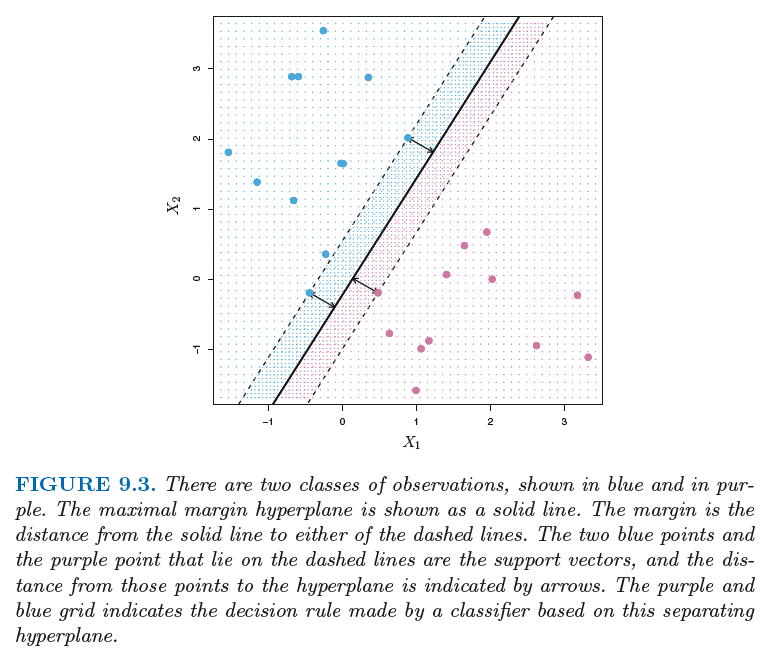
위 그림과 같이 최대 마진 초평면은 관측치와 분리 초평면 사이의 최소거리인 마진이 큰 것을 알 수 있다.
여기서 margin의 폭을 결정하는 점들을 support vetors라고 한다.
왜냐면 이 점들의 이동이 일어나면 hyperplane도 이동하게 될 것이라는 의미에서 maximal margin hyplane을 서포는 하기 때문에 support vetor라고 부른다.
Construction of the Maximal Margin Classifier
Maximal Margin Classifier를 구성하는 방법은 아래 식과 같다.

위 식의 M은 hyperplane과 support vector간의 거리라고 볼 수 있다.
위 식을 자세히보면 점과 직선과의 거리 식과 매우 유사함을 알 수 있다.

아래 그림과 같은 경우에는 hyperplane을 가지고 완벽하게 분리를 할 수 없는데
이때, 비록 모든 관측치를 정확히 분류하지 못하더라도, 최대한 일반화 가능성이 높게끔 하는 최대 마진을 찾는 분류기를 만드는데 이를 소프트 마진 분류기라고 한다.

아래 왼쪽그림은 일반화가 잘된 초평면(hyperplane)을 찾은 것이고, 오른쪽은 그렇지 못한 케이스라고 볼 수 있다.

서포트 벡터 머신은 초평면을 이용하여 생각보다 잘 분류를 하지만 아래 그림과 같이 분류된 관측치가 마진안에 있거나 hyperplane이 분류자체를 제대로 하지 못한 케이스가 있다.
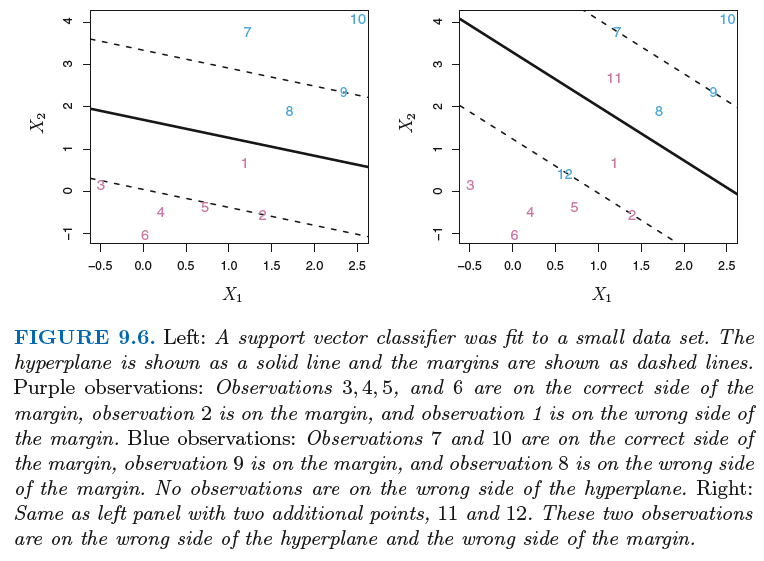
이러한 문제는 현실에서 매우 있을법한 케이스이다.
따라서 마진을 구하는 알고리즘에 관측 데이터가 마진 안쪽 또는 hyperplane을 기준으로 옳지 않은 곳에 있도록 허용하는 slack variable 을 추가한다. (아래식에서는 앱실론이 slack variable)

여기서 C는 slack variable의 합을 한전하는 것으로 허용 범위를 결정하는 튜닝파라미터라고 보면 된다.
즉, hyperplane을 이용하여 분류를 할 때 어느 정도까지 오차를 허용해줄 것이냐를 결정하는 것이라고 생각하면 된다.
따라서, C가 증가함에 따라 margin 위반에 대한 허용 정도가 증가하게 되어 margin의 폭이 넓어질 것이고, C가 감소하면 margin의 크기(폭)도 감소하게 된다.

그러나, 현재까지 본 서포트 벡터는 아래와 같이 비선형적으로 퍼져있는 데이터에 대해서는 분류가 어렵다.

이를 해결하기 위해 나온것이
비선형 결정경계를 가지는 서포트 벡터 머신이다.
Classification with Non-linear Decision Boundaries
아래식처럼 cross feature 나 power를 이용하여 비선형 feature를 만들 수 있다.

커널이라는 개념을 사용한 서포트 벡터 머신의 확장 기능을 이용하면, 선형이든, 비선형이든 효과적으로 분류할 수 있다.
Support Vector Machine
커널의 형태로, 선형과 비선형의 결정경계를 얻어 내는 방법이다.
선형 커널 예
kernel

비선형 커널 예
Polynomial kernel

Radial kernel

적절한 커널의 사용은 분류의 정확도를 높인다.
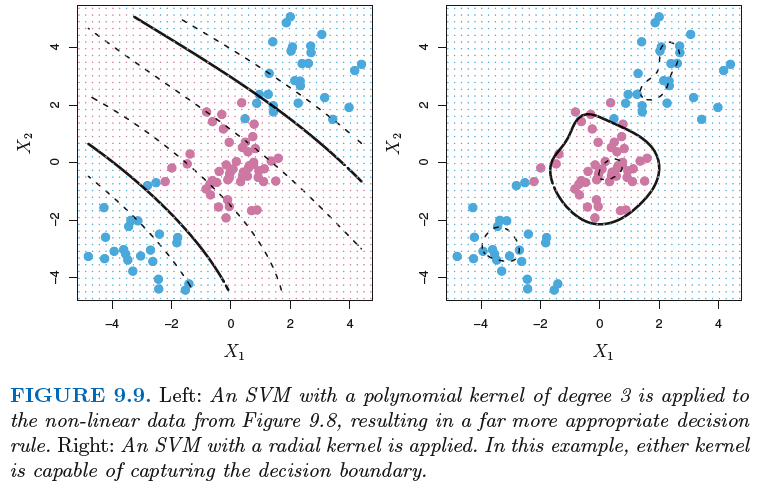
아래 왼쪽 그림은 3차수의 다항식 커널, 오른쪽그림은 radial 커널을 활용한 예이다.
각 모델별(SVM, LDA) 성능을 ROC 커브로 비교하면
training set
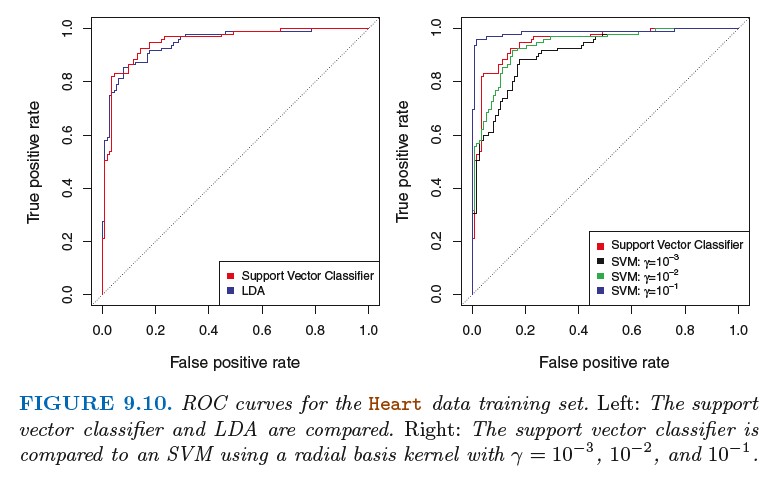
test set

SVMs with More than Two Classes
현재까지는 이진분류에 사용되는 SVM을 알아봤는데
클래스가 3개 이상인 것에 대해서는 어떻게 적용이 가능할까?
크게 두가지 방법으로 나눌 수 있다.
-
One-versus-One
-
One-versus-All
One-Versus-One Classification
SVM을 사용할때 K>2 인 클래스가 있다면
SVM을 kC2 의 경우의 수많큼 모델을 구성하여 한쌍씩 비교하는 것이다.
즉,

만큼의 쌍별 분류를 하여 문제를 마무리한다.
One-Versus-All Classification
총 k개의 클라스가 있다면
일단 1개의 클라스를 선택하고, 나머지 k-1클래스를 다른 하나의 클래스로 판단하여 분리하는 방식이다.
이런식으로 순차적으로 진행하면
다음 단계에서는 k-1개의 클래스에서 하나 클래스 선택하여 분리해나가는 방식이다.
위 방식은 경우의 수가 k*(k+1)/2 정도 될 것 같다.
Relationship to Logistic Regression
결론을 말하자면...형태가 비슷하고, 식에서 패널티를 주는 방식도 비슷,
특히 loss 의 감소를 그래프로 비교했을때 두개의 모델이 매우 유사하다 이다.


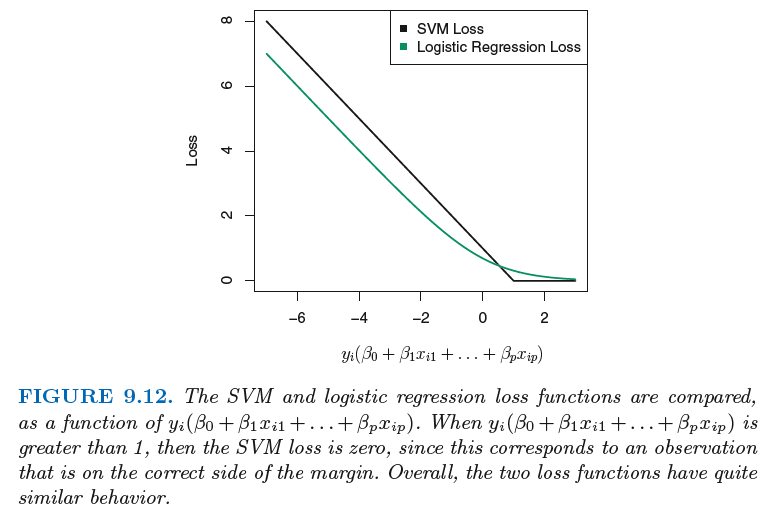
출처 : An Introduction to Statistical Learning in R
'Statistical Learning' 카테고리의 다른 글
| Imbalanced data approach (1) | 2020.08.10 |
|---|---|
| [ISLR] Unsupervised Learning (0) | 2020.04.08 |
| [기초통계] 왜도(Skewness)와 첨도(Kurtosis) (1) | 2020.03.28 |
| [ISLR] Tree-Based Methods (0) | 2020.03.26 |
| [ISLR] Moving Beyond Linearity (0) | 2020.03.19 |




