Timeseries Analysis - statsmodels.tsa

시계열분석을 하기 위해 statsmodels 라는 패키지에 tsa 이용한다.

 

여기서 다루는 내용은 시계열분 중 STL Decompose를 다룬다.

 

 

시계열 분해의 개념은 시계열적인 특성을 띠는 데이터를 trend, seasonal(주기성), residual 로 나누어 분석하는 것이다 (STL Decompose).

 

시계열 분해 모델은 크게 Additive, Mulitiplicative 모델로 나눌수 있다.

 

Additive 모델

말 그대로 origin = trend + seasonal + residual 으로 나누어 분석한 모델이다.

y(t) = Level + Trend + Seasonality + Noise

 

Mulitiplicative 모델

origin = trend * seasonal * residual 으로 나누어 분석한 모델이다.

multiplicative 모델을 활용하려면 데이터에 0이 존재하면 안된다. 왜냐면 0이 존재하면 데이터를 분해할 수가 없기때문이다.

y(t) = Level * Trend * Seasonality * Noise

The additive model is Y[t] = T[t] + S[t] + e[t] The multiplicative model is Y[t] = T[t] * S[t] * e[t]

 

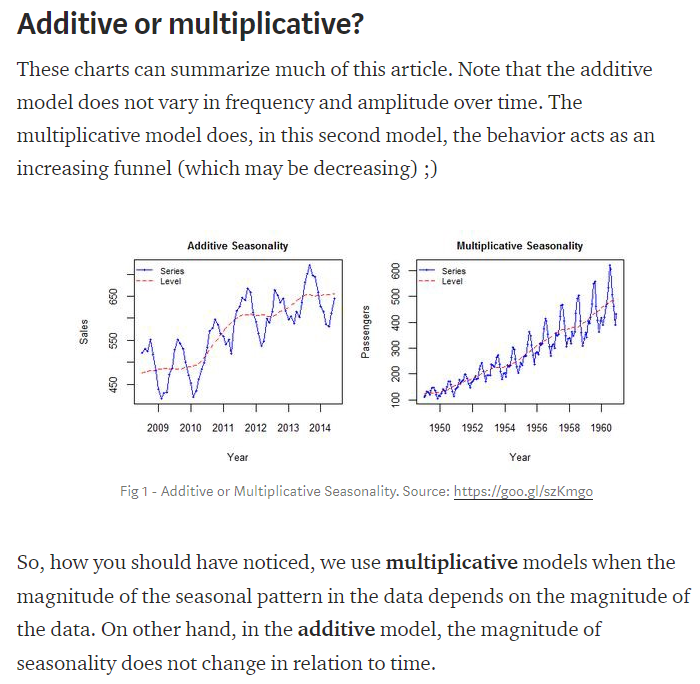
Additive vs Multiplicative

- 이 둘의 가장 큰 차이점은 additive모델은 프리퀀시가 트렌드와 다르다.

특히 장기간의 분석에서는 seasonal data 결과는 트렌드를 따라가지 못해서 적합하지 않다.

- 반면에, multiplicative 모델은 분해값들의 곱인 비율로 이루어져 있어서 트렌드에 맞게 seasonal 데이터가 변화한다.

이는 시간이 지남에 따라 금리가 오르는 현상을 고려할 수 있는 모델로 볼 수 있다.

 

 

source : https://medium.com/@sigmundojr/seasonality-in-python-additive-or-multiplicative-model-d4b9cf1f48a7

 

 

 

그렇다면 trend와 seasonal은 어떻게 구할까?

기본적인 시계열분해의 개념에서는 loess(local regression)을 이용하여 trend를 구한후, 설정한 frequency 주기에 따라 period를 구해 seasonal을 구한다(마찬가지로 loess 이용) --> 결국 moving average를 사용

 

 

statsmodels에서는 moving average를 사용하지만, 아래와 같은 방법론을 다양한 필터로 적용하도록 지원할 모양이었나 보다.

statsmodels.tsa.filters.bk_filter.bkfilter          Baxter-King filter.  statsmodels.tsa.filters.cf_filter.cffilter          Christiano-Fitzgerald asymmetric, random walk filter.  statsmodels.tsa.filters.hp_filter.hpfilter          Hodrick-Prescott filter.  statsmodels.tsa.filters.convolution_filter          Linear filtering via convolution.  statsmodels.tsa.seasonal.STL          Season-Trend decomposition using LOESS.

 

여러 방법을 사용할 것처럼 주석처리해놓았으나...

코드를 살펴본 결과, statsmodels 에서는 convolution 필터를 이용하여 분해한다.

 

그렇다면 statsmodels에 있는 tsa 코드를 쓰는 예제를 한번 살펴보자. 

- freq 는 seasonal을 볼때 주기를 의미함

import matplotlib.pyplot as plt
from statsmodels.tsa.seasonal import seasonal_decompose

result = seasonal_decompose(series, model = 'addictive', freq = 144)
result.plot()
plt.show()

 

 

이미지가 아닌 각 데이터를 추출하고 싶다면 아래처럼!

from statsmodels.tsa.seasonal import seasonal_decompose

result = seasonal_decompose(series, model = 'multiplicative', freq = 144)

result.observed 		## observed 데이터 출력
result.trend 			## trend 데이터 출력
result.seasonal 		## seasonal 데이터 출력
result.resid 			## residual 데이터 출력

 

시계열 분해한 data는 그것 차체만으로 의미가 있을 수 있기 때문에

시계열 분해 데이터는 적재할 필요가 있다.

 

그리고 특정 기간 이전부터 분석시간(job_time)에 대해 유의미한 결과를 얻는 것 중 한 방법은

residual data를 기준으로 현재 데이터가 기간 데이터의 일정 sigma를 넘는 지 판단하는 로직을 통해 이상치를 탐지할 수 있다.

시계열 분해를 한 잔차 데이터(residual)는 정규분포를 따른다.

 

만약 threshold를 6sigma로 설정한다면

6sigma = 평균  + 6 * 표준편차 (threshold 이상을 볼 경우)  --> 기간 데이터로 산정

6sigma = 평균  - 6 * 표준편차 (threshold 이하를 볼 경우)

현재 시점의 residual data가 threshold를 넘는지를 확인하면 된다.

 

시계열 데이터 분해는 시계열에 따라 주기적인 패턴을 갖는 데이터를 분석하는데 아주 용이하다.