정상성과 차분 (stationarity & differencing)

- 정상성(stationarity)을 가지는 데이터란 어떠한 분포 (정규분포 등)을 따르는 데이터를 의미함

좌 : non-stationary, 우 : stationary

정상성 (Stationarity)

- 정상성(stationarity)을 나타내는 시계열은 시계열의 특징이 해당 시계열이 관측된 시간에 무관

- 추세나 계절성이 있는 시계열은 정상성을 나타내는 시계열이 아님

- 추세와 계절성은 서로 다른 시간에 시계열의 값에 영향을 줄 것이기 때문

- 반면에, 백색잡음(white noise) 시계열은 정상성을 나타내는 시계열

  > 언제 관찰하는지에 상관이 없고, 시간에 따라 어떤 시점에서 보더라도 똑같이 보일 것

 

몇 가지 경우는 헷갈릴 수 있습니다

— 주기성 행동을 가지고 있는 (하지만 추세나 계절성은 없는) 시계열은 정상성을 나타내는 시계열입니다. 왜냐하면 주기가 고정된 길이를 갖고 있지 않기 때문에, 시계열을 관측하기 전에 주기의 고점이나 저점이 어디일지 확실하게 알 수 없습니다.

일반적으로는, 정상성을 나타내는 시계열은 장기적으로 볼 때 예측할 수 있는 패턴을 나타내지 않을 것입니다. (어떤 주기적인 행동이 있을 수 있더라도) 시간 그래프는 시계열이 일정한 분산을 갖고 대략적으로 평평하게 될 것을 나타낼 것입니다.

 

예시)

Figure 8.1: 다음의 시계열 중에서 어떤 것이 정상성을 나타낼까요? (a) 200 거래일 동안의 구글 주식 가격; (b) 200 거래일 동안의 구글 주식 가격의 일일 변동; (c) 미국의 연간 파업 수; (d) 미국에서 판매되는 새로운 단독 주택의 월별 판매액; (e) 미국에서 계란 12개의 연간 가격 (고정 달러); (f) 호주 빅토리아 주에서 매월 도살한 돼지의 전체 수; (g) 캐나다 북서부의 맥킨지 강 지역에서 연간 포획된 스라소니의 전체 수; (h) 호주 월별 맥주 생산량; (i) 호주 월별 전기 생산량.

 

그림 8.1에 나타낸 9개의 시계열을 살펴봅시다. 이 중에서 어떤 것이 정상성을 나타내는 시계열이라고 생각합니까?

분명하게 계절성이 보이는 (d), (h), (i)는 후보가 되지 못합니다.

추세가 있고 수준이 변하는 (a), (c), (e), (f), (i)도 후보가 되지 못합니다.

분산이 증가하는 (i)도 후보가 되지 못합니다. 

 

(b)와 (g)만 정상성을 나타내는 시계열이다.

 

언뜻 보면 시계열 (g)에서 나타나는 뚜렷한 주기(cycle) 때문에 정상성을 나타내는 시계열이 아닌 것처럼 보일 수 있습니다. 하지만 이러한 주기는 불규칙적(aperiodic)입니다 — 먹이를 구하기 힘들만큼 살쾡이 개체수가 너무 많이 늘어나 번식을 멈춰서, 개체수가 작은 숫자로 줄어들고, 그 다음 먹이를 구할 수 있게 되어 개체수가 다시 늘어나는 식이기 때문입니다. 장기적으로 볼 때, 이러한 주기의 시작이나 끝은 예측할 수 없습니다. 따라서 이 시계열은 정상성을 나타내는 시계열입니다.

 

시계열 데이터를 정상성을 가지도록 만드는 방법 : 차분, 로그변환, box-cox변환

차분 (Differencing)

그림 8.1의 패널 (a)의 구글(Google) 주식 가격이 정상성을 나타내는 시계열이 아니었지만 패널 (b)의 일별 변화는 정상성을 나타냈다는 것에 주목합시다.

이 그림은 정상성을 나타내지 않는 시계열을 정상성을 나타내도록 만드는 한 가지 방법을 나타냅니다 — 연이은 관측값들의 차이를 계산하는 것입니다. 이것은 차분(differencing)로 알려져 있습니다.

로그 같은 변환은 시계열의 분산 변화를 일정하게 만드는데 도움이 될 수 있습니다.

차분(differencing)은 시계열의 수준에서 나타나는 변화를 제거하여 시계열의 평균 변화를 일정하게 만드는데 도움이 될 수 있습니다. 결과적으로 추세나 계절성이 제거(또는 감소)됩니다.

정상성을 나타내지 않는 시계열을 찾아낼 때 데이터의 시간 그래프를 살펴보는 것만큼, ACF 그래프도 유용합니다. 정상성을 나타내지 않는 데이터에서는 ACF가 느리게 감소하지만, 정상성을 나타내는 시계열에서는, ACF가 비교적 빠르게 0으로 떨어질 것입니다. 그리고 정상성을 나타내지 않는 데이터에서 r1r1은 종종 큰 양수 값을 갖습니다.

Figure 8.2: 구글 주식 가격의 ACF (왼쪽) 그리고 일별 변동 (오른쪽).

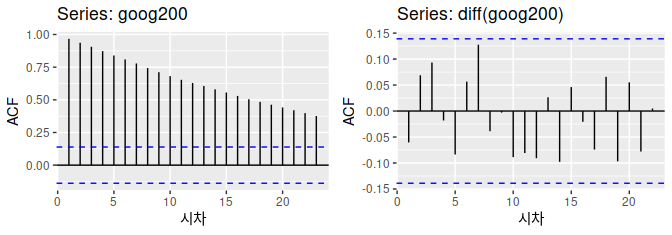
Box.test(diff(goog200), lag=10, type="Ljung-Box")
#> 
#> 	Box-Ljung test
#> 
#> data:  diff(goog200)
#> X-squared = 11, df = 10, p-value = 0.4

차분을 구한 구글 주식 가격의 ACF는 단순히 백색잡음(white noise) 시계열처럼 생겼습니다.

95% 한계 바깥에 자기상관(autocorrelation) 값이 없고, 융-박스(Ljung-Box) Q∗ 통계는 h=10 에 대해 0.355라는 p-값을 갖습니다. 이 결과는 구글 주식 가격의 일별 변동이 기본적으로는 이전 거래일의 데이터와 상관이 없는 무작위적인 양이라는 것을 말해줍니다.

 

차분을 수식을 통해 정의하면 다음과 같습니다.

 

Δyt = yt−y(t−1)

첫 번째 관측값에 대한 차분 Δy1을 구할 수 없기 때문에, 차분값들은 T−1개의 값만 가지게 됩니다.

2차 차분

가끔 차분을 해도 시계열의 정상성이 만족되지 않는 경우도 있습니다. 그럴 경우, 정상성을 나타내는 시계열을 얻기 위해 다음과 같이 한 번 더 차분을 구하는 작업이 필요할 수도 있습니다.

Δyt−Δyt−1=(yt−yt−1)−(yt−1−yt−2)=yt−2yt−1+yt−2

이 경우 2차 차분값은 T−2T−2개의 값을 가지게 됩니다. 결국, 2차 차분은 원본 시계열 데이터의 “변화에서 나타나는 변화”를 모델링하게 되는 셈입니다. 실제 상황에서는 2차 차분 이상으로 구하는 경우는 거의 일어나지 않는다 합니다.

계절성 차분

계절성 차분은 관측치와, 같은 계절의 이전 관측값과의 차이를 말합니다. 따라서 다음과 같이 정의가 됩니다.

yt − y(t−m)

여기서 m은 주기에 해당합니다. 즉 m=12이고 월별로 집계된 값이라면, 올해 1월의 값 - 작년 1월의 값, 올해 2월의 값 - 작년 2월의 값, … 이 되겠죠.

 

출처 : https://otexts.com/fppkr/stationarity.html

Forecasting: Principles and Practice

https://assaeunji.github.io/statistics/2021-08-08-stationarity/