| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- session 유지
- BigQuery
- integrated gradient
- requests
- subdag
- login crawling
- 공분산
- gather_nd
- spark udf
- grad-cam
- 상관관계
- hadoop
- Airflow
- UDF
- Counterfactual Explanations
- Retry
- tensorflow text
- XAI
- youtube data
- 유튜브 API
- chatGPT
- top_k
- TensorFlow
- API
- flask
- GCP
- correlation
- GenericGBQException
- airflow subdag
- API Gateway
- Today
- Total
데이터과학 삼학년
[기초통계] R-square 본문
그 중에서도 제일 와 닿았던 부분은 R-square에 대한 내용이다.
어렴풋하게 알고 있던 내용을 직관적으로 와닿게 설명하고 있어서, 여기에 정리해본다.
아래 PPT는 Data Analysis with Python에서 발췌한 내용이다.

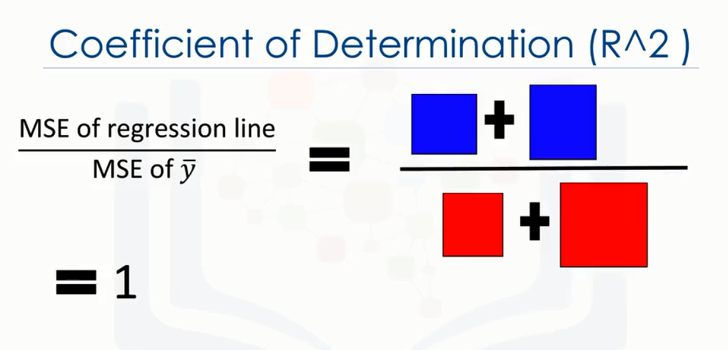
R-square은 평균 제곱 오차, MSE (Mean squared error) 로부터 계산된다.
즉 1-(추정 모형의 MSE / 평균 관측 값의 MSE) 이다.

위 그림에서 파란 선은 회귀선(Regression line), 파란 박스는 회귀선의 MSE,
빨간 선은 관측 데이터 모형(data point), 빨간 박스는 관측 데이터 모형의 MSE 이다.
위 그래프에서 보면 파란 박스의 면적이 빨간 박스보다 작은 것을 알 수 있다.
즉, 회귀선(Regression line)의 MSE 값이 작다.

이것을 R-square의 1- 부분을 제외한 식에 대입하면,
분모가 분자보다 더 크게 된다.
파란 박스가 빨간 박스보다 훨씬 작고, 즉 MSE는 작으므로 분자는 작다.
심플하게 이야기하면 관측 데이터 평균의 MSE가 회귀선의 MSE보다 큰 것이며,
위 식이 0에 가까운 값이 되는 것이다. 결국 R-square은 아래와 같이 1에 가까운 값이 된다.

이 때의 R-square가 1에 가깝다는 의미는
바꿔 말하면 이 회귀선은 데이터에 fit한 것을 알 수 있다.

반대로, 이번엔 빨간 박스보다 파란 박스의 면적이 더 넓다.
이전과 비교하여 파란 박스, 회귀선(Regression line)의 MSE가 더 커졌다.
파란 박스와 비교하여 빨간 박스의 면적이 거의 동일하다는 것을 알 수 있다.
분자가 커지게 되므로, 위 식은 1에 가까운 값이 된다.
즉, 전체 식인 R-square은 0에 가깝게 된다.

이 때의 R-square가 0에 가깝다는 의미는
바꿔 말하면 회귀선의 설명력(Regression line)이 낮다는 의미가 되며, 데이터가 모형에 fit하지 않음을 뜻한다.
오차의 정도를 박스로 표현하여, 분모 분자에 대입하는 형태로 비교하니 훨씬 쉽게 감이 잡혔다.
심플하게 이야기하면,
설계한 모형의 오차가 작다면 R-square가 커지게 될 것이고, 설계한 모형의 오차가 크다면 R-square가 작아지게 되는 것이다.
출처: https://jinchory.tistory.com/332 [jinchory's blog]
>>즉 baseline model 에 비해 현 모델이 얼마나 정확성을 갖는지를 나타내는 척도라고 보면 됨
- Regression model의 성능을 측정하기 위해 mean value로 예측하는 단순 모델(Zero-R 모델)과 비교, 상대적으로 얼마나 성능이 나오는지를 측정함. (다른 성능 지표인 RMSE나 MAE는 데이터의 scale에 따라서 값이 천차만별이기 때문에, 절대 값만 보고 바로 판단하기가 어려움.)

( 보통의 경우 0<= R^2 <= 1 , 0이면 0점, 1이면 100점)
출처: https://newsight.tistory.com/259 [New Sight]
'Statistical Learning' 카테고리의 다른 글
| [기초통계] t-statistic, p-value, F-statistic (1) | 2020.02.10 |
|---|---|
| [기초통계] 잔차와 오차 (0) | 2020.02.05 |
| 구조방정식(structural equation modeling, SEM) (0) | 2020.02.04 |
| [기초통계] 통계적 분석방법 (0) | 2020.02.04 |
| [ISLR] Statistical Learning (0) | 2020.02.03 |




