| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- integrated gradient
- GCP
- session 유지
- Airflow
- subdag
- 상관관계
- GenericGBQException
- hadoop
- top_k
- UDF
- API Gateway
- TensorFlow
- 유튜브 API
- gather_nd
- requests
- tensorflow text
- 공분산
- login crawling
- youtube data
- grad-cam
- Counterfactual Explanations
- API
- airflow subdag
- spark udf
- Retry
- flask
- BigQuery
- correlation
- chatGPT
- XAI
- Today
- Total
데이터과학 삼학년
[ISLR] Statistical Learning 본문
Statistical Learning : data를 통해서 pattern을 찾고, 해석가능한 형태의 모델을 구축함으로써 예측(회귀)이나 분류 문제 등을 풀어내는 통계적인 방법이라 이해됨
가령 한 제품의 판매수를 예측하기위해 TV, Radio, Newspaper의 광고와의 인과관계를 본다고 하면
각 X는 Y와 선형적인 관계를 가지고 있고, 그렇다면 위 3개 광고를 동시에 고려하여 판매수를 예측한다면 어떨까?
라는 개념이다.

어떤 변수를 가지고 모델을 만드는 방법은 크게 두가지(Parametric, Non-Parametric)로 나눌 수 있다.
-
Parametric model : 모델의 형태를 가정하고, 데이터를 통해(학습을 통해) 각 파라미터를 추정하여 모델을 완성(lr, LDA, Naive Bayes, 단순 신경망)
-
Non-Parametric model : 모델의 형태가 어떨 것이라는 것을 미리 가정하지 않고 추정하는 방법(KNN, Decision Tree, Boosting/Random Forest, SVM, 복잡 신경망)
모델의 해석도와 모델의 flexibility 정확도(복잡도)의 관계는 아래 그림과 같다.

이렇게 데이터를 통해 모델을 만들고, 이것을 이용하여 문제를 풀지만, 모델은 완벽할 수 없다.
즉 모델은 어쩔 수 없이 줄일 수 없는 오차가 있다는 개념(Irreducible error)이 있다.

그렇다면 우리는 이러한 모델의 오차를 통해서 모델을 평가하고, 어떤 모델을 선택할지 판단이 필요하다.
여기서 나오는 개념이 bias-variance trade off 개념이다.(underfit-overfit)
-
Bias : 모델의 예측값과 실제값과 차이라고 보면 된다. 즉 bias가 크다는 것은 모델이 실제값을 잘 예측하지 못하고 있다는 의미(정확도와 가까운 개념) --> 추정치와 실제값을 이용해 계산
-
Variance : 다른 training data set을 이용해 다시 모델을 학습시킬때 그 예측한(추정된) 결과 값의 변화량을 의미 --> 즉 model이 특정 dataset에 대해 overfit 되었다면 다른 dataset에 대한 결과는 이전의 결과와 상이할 것이다. variance가 높다는 것은 overfit이 되었다는 것으로 보면 된다 --> 추정치만 이용해 (잔차) 계산



이렇게 여러 케이스를 나누며 test error를 비교하게 된다.
이때 Error를 구하는 방법 또한 많다. MSE, RMSE, Cross-entropy error 등등
분류문제를 통해 bias-variance trade off의 중요성을 확인해보자.
예를 들어 KNN의 K 값을 조절하며 확인한 예제를 보면
K=1일때는 Overfit이 되고,,K=100이면 Underfit이 되는 현상이다..이때 적절한 K값을 이미지를 통해 보면 10 정도로 보인다.

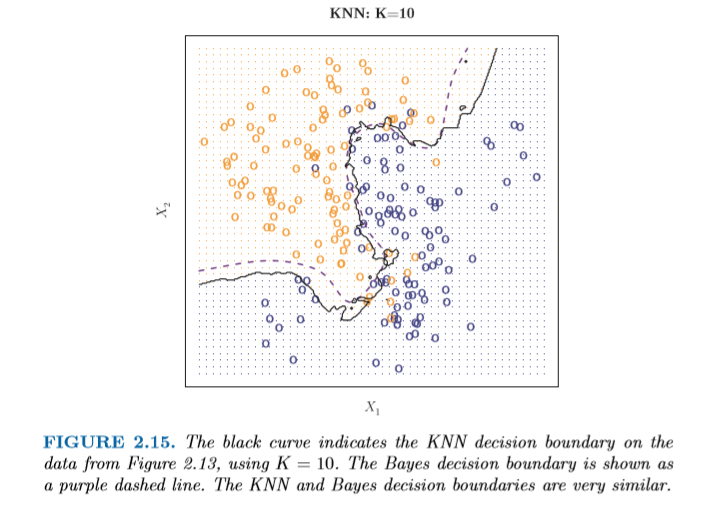
인용 : https://github.com/hyunblee/ISLR-with-Python, An Introduction to Statistical Learning with Applications in R
'Statistical Learning' 카테고리의 다른 글
| [기초통계] t-statistic, p-value, F-statistic (1) | 2020.02.10 |
|---|---|
| [기초통계] 잔차와 오차 (0) | 2020.02.05 |
| 구조방정식(structural equation modeling, SEM) (0) | 2020.02.04 |
| [기초통계] 통계적 분석방법 (0) | 2020.02.04 |
| [기초통계] R-square (0) | 2020.02.04 |




