Mahalanobis Distance

Mahalanobis Distance

- 마할노비스 거리는 다변량 공간에서 2 points 사이의 거리를 의미한다.

- 더 정확히 말하자면 두 변수간의 상관관계까지 고려한 distance를 의미함

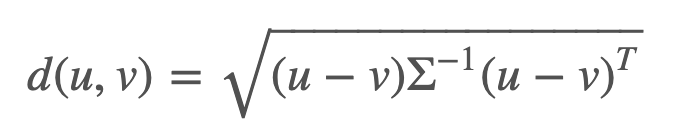
  > 여기서, u는 각 데이터(raw), v는 각 데이터의 평균을 의미한다

  > 예를 들어, 다변량 키, 몸무게가 있다면

        u = (키1,몸무게1)

        v = (키 평균, 몸무게 평균)

    식에서 알 수 있듯이 공분산 매트릭스를 이용하여 거리를 재는 개념이므로,

    다변량 (예, 키,몸무게) 간에 독립이라면 마할노비스 거리는 유클리디안 거리와 동일하다.

 

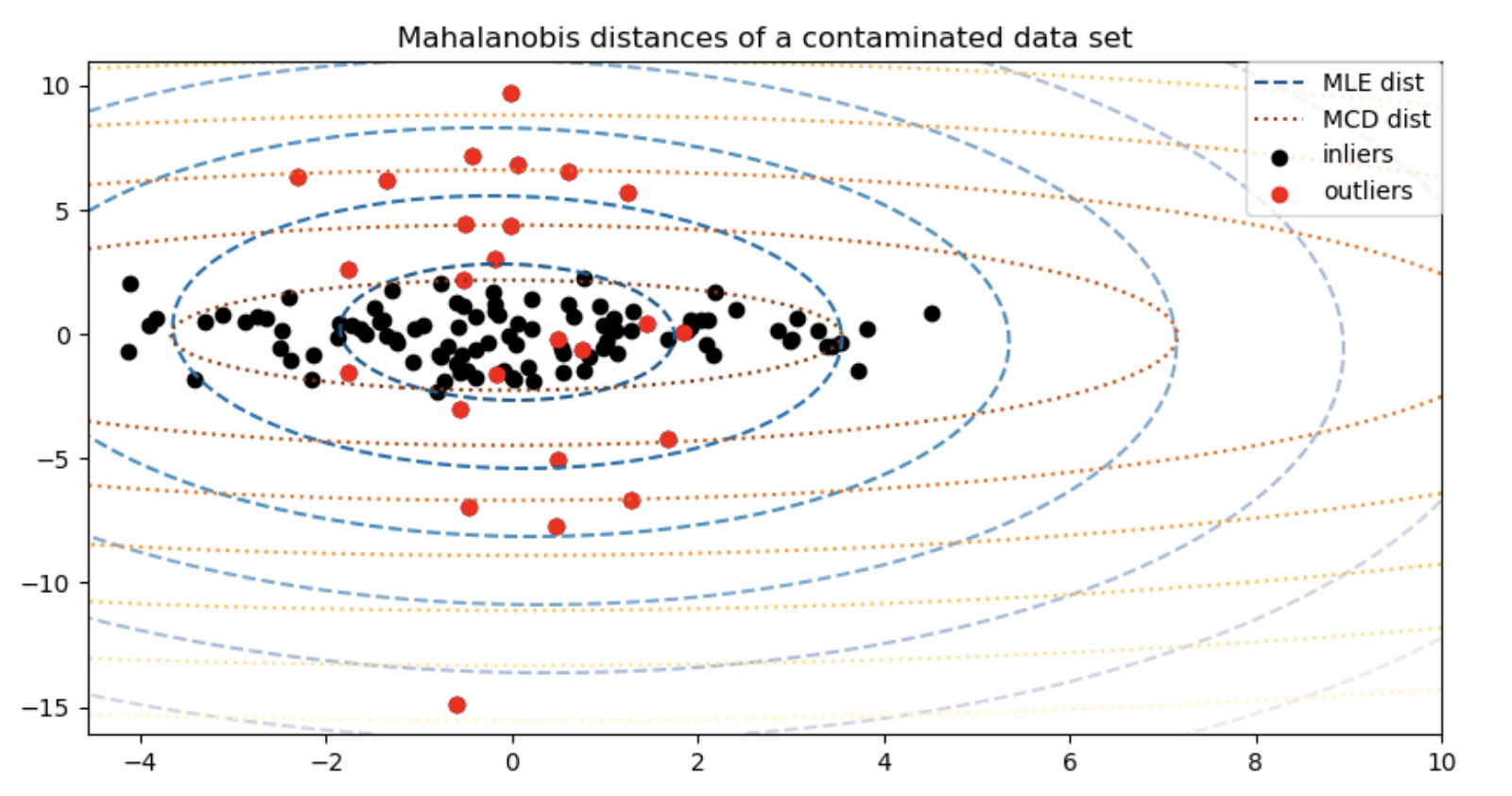
- MCD 기반 Mahalanobis 거리는 내부 검은 색 점에 훨씬 더 잘 맞는 반면 MLE 기반 거리는 특이 치 빨간색 점의 영향을 더 많이 받는 것을 아래 그림에서 확인할 수 있음

적용

- 대부분 다변량 데이터에서 이상치를 탐색하기 위해 주로 사용 --> (Fast-MCD 를 이용)

 

단점

- 데이터에 outlier 가 있을때, 공분산 매트릭스가 오염되게 되어 마할노비스 거리는 잘못 추정될 수 있다.

  > 이를 보완하기 위해 나온 것이 MCD (Minimum Covariance Determinant estimator)

 

 

MCD (Minimum Covariance Determinant estimator)

- 데이터에서 h개의 샘플 데이터를 뽑아서 공분산이 가장 작은 데이터를 선정해 평균, 표준편차를 구해 마할노비스 거리를 산정하는 방법

- MCD를 이용하면 아래 그림 처럼 이상치 분포를 확실히 더 잘 구분한 것을 알 수 있음

 

 

scikit-learn.org/stable/auto_examples/covariance/plot_mahalanobis_distances.html#sphx-glr-auto-examples-covariance-plot-mahalanobis-distances-py