| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- correlation
- top_k
- 유튜브 API
- GCP
- Counterfactual Explanations
- Retry
- youtube data
- XAI
- tensorflow text
- BigQuery
- hadoop
- TensorFlow
- 상관관계
- spark udf
- grad-cam
- login crawling
- airflow subdag
- GenericGBQException
- requests
- subdag
- session 유지
- 공분산
- UDF
- Airflow
- gather_nd
- API
- chatGPT
- API Gateway
- flask
- integrated gradient
- Today
- Total
데이터과학 삼학년
Multivariate recurrence plots (2004) 본문
Multivariate recurrence plots (2004)
Abstract
- multivariate timeseries data를 recurrence plots 으로 계산하는 접근법에 대한 제시 (joint recurrences 를 기반)
- entropy 를 측도로 이용하여 연구 (joint Rényi entropy)
-
양방향의 무질서한 시스템 동기화
-
전이(변하는 지점)을 찾기 위함
1. Introduction
- 궤적 데이터의 행동을 시각화 하는 방법 → Recurrence plots (RP)
- 두개의 다른 동적 시스템 사이의 관계를 나타내기 위해 진화된 버전이 cross recurrence plot (CRP)
- non-stationary 하고, 짧은 주기의 시계열 데이터에도 적용 가능
- 위 논문에서는 다음과 같은 순으로 outlines
-
multivariate RPs 의 필요성과, Rényi entropy 추정 소개
-
잠재성 증명을 위해 동일하지 않은 다른 두개 데이터로 적용
-
제안된 방법인 PS(phase synchronization) 탐지와 전체 시스템의 세부적 구조를 확인할 수 있음을 확인
2. Multivariate recurrence plots
- 정보의 양(선형, 비선형 종속성)을 수량화할 수 있음 (auto, respectively, cross mutual information)
- 두개의 궤도 (x,y) 가 있다면, 이 두개의 동적 시스템을 확률 분포를 이용해 표현할 수 있음
- 이 두개를 동시에 나타내는 joint probability 분포를 만들 수 있음

여기서, H2 는 Rényi information 임
- H2를 아래 식(2) 와 같으며,식(2)를 이용하여 GMI를 다시 나타내면 식(3) 과 같음

- 위 식(4) 는 time delay를 포함하여 GMI 를 다시 나타낸 것
- AMI (auto mutual information)은 아래 식(5) 와 같음

- H2는 결국, RP 매트릭스를 이용하여 나타낼수 있고, 추정된 joint Rényi information 는 식(8) 과 같음

- 위 로직을 다시 x,y 에 대한 RP 매트릭스를 이용하여 나타내면 식(9) 와 같음

- 식(9)에 time delay를 반영하면 식(10)과 같이 나타낼 수 있음

- joint recurrence matrix 는 식(11)과 같다

- 위에서 제안된 식(11) 과 같은 joint recurrence matrix를 Multivariate recurrence plot (MRP)로 제안함
3. Estimation of the joint Rényi entropy of second order
- joint Rényi entropy 는 아래 식(12) 와 같이 나타낼 수 있음

- 식(12)를 Joint Recurrence matrix를 통해 재 추정 가능한데, 이는 식(13)과 같음

- 위의 괄호안의 식은 MRP의 최소 대각 라인 길이를 의미
> 이를 통해 대각 길이의 히스토그램을 만들 수 있음
- 대각 길이 l 을 가로, 세로축으로 분포의 기울기는 joint Rényi entropy 를 의미하게 됨
> 이것이 MRPs의 분석적 큰 장점이라고 볼 수 있음
4. Detection of synchronization transition by means of joint recurrences
- Phase synchronization을 이용
- u, v를 통해 tuning 가능

- fig.1 에서 mean frequencies 평균 차이를 통해 나타낸 것...

- joint entroy로 MRPs 구성

- Sum of the positive Lyapunov exponents of the two Rössler oscillators 로 MRPs 구성


5. Conclusions
- joint recurrence 를 기반으로 한 MRPs 는 쉽게 joint Rényi entropy of second order K2 를 추정할 수 있음
- 이 논문에서 제안하는 MRPs 방법은 총 3가지
-
Difference |Ω| between the mean frequencies of the two Rössler oscillators
-
Sum of the positive Lyapunov exponents of the two Rössler oscillators
-
Joint Rényi entropy Kˆ2 of the two Rössler oscillators
- 모두 비슷한 spectrum의 구조를 나타냄

참조: ROMANO, M. Carmen, et al. Multivariate recurrence plots. Physics letters A, 2004, 330.3-4: 214-223.
'Papers' 카테고리의 다른 글
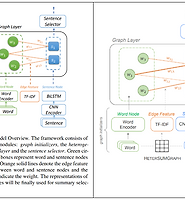
| Heterogeneous Graph Neural Networks for Extractive Document Summarization (2020) (0) | 2022.05.06 |
|---|---|
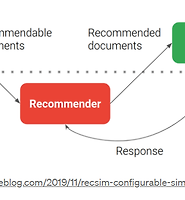
| RECSIM: A Configurable Simulation Platform for Recommender System (2019) (0) | 2021.06.02 |
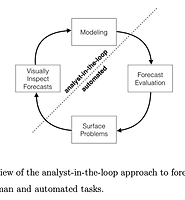
| Forecasting at Scale (2018) - Prophet 소개 (0) | 2020.12.10 |
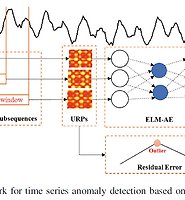
| Anomaly Detection in Time Series Data Based on Unthresholded Recurrence Plots (2018) (0) | 2020.12.02 |
| Universal Sentence Encoder (2018) (0) | 2020.08.06 |