| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- grad-cam
- Retry
- hadoop
- XAI
- 유튜브 API
- login crawling
- chatGPT
- 공분산
- Counterfactual Explanations
- top_k
- Airflow
- airflow subdag
- UDF
- spark udf
- 상관관계
- session 유지
- TensorFlow
- requests
- API
- API Gateway
- youtube data
- tensorflow text
- gather_nd
- correlation
- flask
- BigQuery
- GCP
- subdag
- GenericGBQException
- integrated gradient
- Today
- Total
데이터과학 삼학년
Forecasting at Scale (2018) - Prophet 소개 본문
Forecasting at Scale (2018) - Prophet 소개
|
Abstract 1 Introduction 2 Features of Business Time Series 3 The Prophet Forecasting Model 3.1 The Trend Model 3.1.1 Nonlinear, Saturating Growth 3.1.2 Linear Trend with Changepoints 3.1.3 Automatic Changepoint Selection 3.1.4 Trend Forecast Uncertainty 3.2 Seasonality 3.3 Holidays and Events 3.4 Model Fitting 3.5 Analyst-in-the-Loop Modeling 4 Automating Evaluation of Forecasts 4.1 Use of Baseline Forecasts 4.2 Modeling Forecast Accuracy 4.3 Simulated Historical Forecasts 4.4 Identifying Large Forecast Errors 5 Conclusion |
Abstract
- forecasting은 데이터 사이언스의 공통 업무이며, 주로 목표 설정, 이상탐지, 용량 설정 등을 할 수 있도록 도움
- 그럼에도 불구하고, 시계열 모델링에 대한 전문가는 극히 적음
-
완전 자동화 되는 시계열 튜닝 어려움
-
도메인지식을 가지고 있으면서 시계열 분석에 대한 지식이 있는 사람 적음
- scale은 analyst-in-the-loop 모델의 예측 결과를 비교 평가하고, 자동으로 플래그를 지정하는 방식
-modular regression model 을 이용해서 분석가가 직관적으로 조정할 수 있는 파라미터가 있는 모델을 구성함
1 Introduction
- 높은 품질의 예측은 매우 어려운 일임
-
완전한 자동화 예측 기술은 튜닝하기 매우 어려울 수 있고, 유연하지 않은 경우가 많음
-
도메인 지식 전문가는 시계열 예측에 대한 전문적인 지식을 갖고 있지 않은 경우가 많음
- 위와 같은 이유로 prophet을 만듦(제안하는 scale의 개념)
-
많은 사람들이 교육없이 시계열 예측을 할 수 있게 함
-
특이한 feature로 인해 잠재적인 다양한 예측 문제 존재
-
분석가가 모델을 보고 무엇이 잘못되었는지 이해하고, 필요한 조정을 할 수 있도록 함
-
많은 예측 결과가 만들어지고 이를 평가하고 비교, 그리고 human feedback을 통해 스스로 문제를 해결하게 함
-
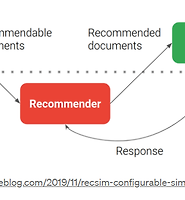
시뮬레이션 평가시스템은 아래 그림과 같음
-
핵심은 낮은 성능을 보일때 잠재적인 문제에 대해 우선적으로 flag를 걸어둠
-
이를 통해 분석가는 해당문제에 대해 조사하고, 그것을 반영하여 모델을 조정할 수 있음

2 Features of Business Time Series
- 비즈니스 예측 문제는 매우 다양하지만, 그 데이터들은 공통된 특징이 있음
- 아래 그림은 facebook 시계열 데이터를 나타낸 그림
-
시계열 데이터에서 보이는 특징은 주별/ 연별 주기성, 특정 이벤트 발생(연말효과), 이상치
-
새로운 상품이나 마켓변화에 의한 시계열 변화

- figure 3 은 과거 시계열적인 특성을 반영하여 분석한 몇몇의 분석 예를 나타내고 있음
-
automatic ARIMA 모델은 최근 trend의 변화(cutoff)가 있을때 제대로 반영하지 못함
-
exponential smoothing (ets) 와 seasonal naive forecast(snaive)는 주 단위 주기성은 잡았지만, 더 긴기간에 대해서는 miss
-
아래의 모든 케이스는 연말효과에 대해 과대 반응을 보이게 됨
-
이를 통해 이러한 모델은 연간, 계절간 모델로 적용하기에는 부적절하기 때문
-
이러한 문제를 해결하기 위해서는 hyperparameter tune (예컨대 주기단위 등)이 필요함 → 그러나, 이것은 깊은 도메인지식을 필요로 함
-
특히, arima의 경우, 파라미터 조정을 위해 자기회귀, ma, 차분 등 알아야할 것도 많음

3 The Prophet Forecasting Model
- 앞에서 다룬 시계열 예측 모델의 문제들을 해결하기 위해 새로운 시계열 예측 방법(Prophet)을 개발
- 기본 아이디어는 시계열 분해 모델임
-
trend, seasonality, holidays

-
g(t)는 반복적인 요소를 가지지 않은 트렌드
-
s(t)는 요일 혹은 연 계절성과 같은 반복적인 변화
-
h(t)는 Holiday와 같이 가끔씩 불규칙하게 영향을 미치는 요소
-
e는 정규분포를 따르는 잔차로 가정
- GAM 모델 (Generalized Additive Model) 과 비슷
-
새로운것이 발견되었을때 다시 모델을 쉽게 훈련할수 있다는 장점 (L-BFGS참조)
-
Prophet이라는 모델은 문제에 curve-fitting (문제를 잘 반영할 수 있도록 커브를 그리는 것) 초점
-
ARIMA처럼 inferential 한 이점을 가지고 가지는 않음
- 이점
-
유연성 : 계절성과 여러 기간들에 대한 예측을 쉽게 모델에 적용
-
ARIMA모델과 다르게, 모델을 차분해서 정규화 시킬필요도 없고 결측치들을 만들어 넣을 이유가 없음
-
학습이 빠르고 분석가는 여러가지 상세한 모델 스펙을 평가 가능
-
결국에는 회귀분석과 매우 유사하여 생소한 시계열 분석보다 빠르게 적응
3.1 The Trend Model
- trend model 로 saturating growth model, piecewise linear model 사용
3.1.1 Nonlinear, Saturating Growth
- growth (성장) 예측을 위해서 핵심요소는 얼마나 population이 성장할것이고, 얼마나 지속될 것인가 임
- facebook 에서의 성장 모델링은 실제 자연 생태계에서의 인구성장 모델과 매우 유사함
- nonlinear 성장이 있는데 이는 수용가능한 용량에 영향을 받음 (saturating growth)
-
페이스북 유저 수는 인터넷에 접근할 수 있는 사람들 수 안에 있음

-
C : carrying capacity, k : growth rate, m : an offset parameter
- 성장률에 대해서는 중요한 2가지가 있음
-
용량은 상수가 아니다. → 시간에 따라 계속해서 변하게 된다
-
시간이 지날 수록 인터넷에 접근할 수 있는 사람들은 증가할 것이기 때문
-
이를 반영하기 위해 C를 시간에 대해 변화할 수 있는 time-varying capacity C(t). 로 대체
-
성장률 역시 상수가 아니다.
-
새로운 프로덕트가 나오게 되면, 성장률이 대체될 수 있음
-
모델은 역사적인 데이터를 맞추기위해 다양한 rate를 통합해야함
- 이러한 트렌드 변화를 성장 모델에서 통합했음
-
changepoints : 성장률이 변할 것이라고 생각되는 지점을 정의

- 결국 최종적인 piecewise logistic 성장 모델은 아래 식과 같음

- 여기서 중요한 요인인 C(t) 는 해당 도메인 전문가는 알고 있음
-
market size, 인구 예측 등 (world bank)
>> non linear 성장 모델은 결국 sigmoid curve 로 표현
3.1.2 Linear Trend with Changepoints
- 성장 모델에 포화상태가 일어나지 않는 경우, 즉 용량이 제한되지 않은 경우는 간단하게 linear로 풀 수 있음

-
k is the growth rate, δ has the rate adjustments, m is the offset parameter,
-
γj is set to −sjδj to make the function continuous.
3.1.3 Automatic Changepoint Selection
- changepoint는 분석가에 의해 정의 될 수 있음
-
프로덕트 론칭 일나
-
특정 이벤트 변경일
-
자동적으로 후보군을 선정할 수도 있음
- automatic selection 은 자연스럽게 행해질수 있음 위 식(3),(4)의 조정률을 통해서
- 종종 많은 수의 changepoints를 잡곤 함
-
예를 들면, 특정 연의 모든 한달마다
-
이전의 조정률과 라플라스(laplace)를 사용
- Laplace 변환을 이용
Laplace(0,τ). The parameter τ directly controls the flexibility of the model in altering its rate. Importantly, a sparse prior on the adjustments δ has no impact on the primary growth rate k, so as τ goes to 0 the fit reduces to standard (not-piecewise) logistic or linear growth.
3.1.4 Trend Forecast Uncertainty
- 모델이 외삽(extrapolated) 될때(과거의 데이터를 가지고 fit), 트렌드는 일정한 비율을 가질 것임
- 여기서, 예측의 불확실성을 추정할 필요가 있음 → 보다 일반적인 모델로 확장하기 위해


- 라플라스를 이용해서 평균 changepoints빈도, 즉 미래의 changepoints를 설정할 수 있음
- 즉, 미래에 과거와 같은 평균의 빈도와 변화가 있을 것이다라는 가정으로 불확실성을 측정할 수 있음
3.2 Seasonality
- multi-period seasonality 는 존재함
-
1주일에 5일 일하는 주기
-
여름방학 등
- 이러한 빈도주의 적인 특성을 모델에 반영할 필요가 있음
- Fourier series는 이러한 주기적 효과를 유연하게 하는 모델을 제공함
- 아래 식에서 P는 주기를 의미함
-
p=365.25 라면 1년 주기의 데이터
-
p=7 이라면 1주일 주기의 데이터를 의미함

- 위 식을 이용하여 데이터 x를 구하면

3.3 Holidays and Events
- holidays 와 events 역시 시계열에 다소 큰 영향을 미칠 수 있는 요소임
-
추수감사절, 수퍼볼, 블랙프라이데이 등
- 과거 데이터에서 특정 이벤트가 있는 것들의 리스트를 넣을 수 있고, 과거의 데이터를 통해 이를 반영하게 만듦
- 아래 표처럼 특정 이벤트에 대한 통합적인 데이터를 만들 수 있음


3.4 Model Fitting
- seasonality, holiday에 대한 정보가 matrix X / changepoints 대한 정보가 matrix A 에 담아 놓음 → 위 데이터를 조합해서 모델을 구성함
- model fitting 을 위해 Stan’s L-BFGS 을 사용함

- 위 처럼 모델을 fitting 하고 난 결과를 그림으로 표현한 결과는 아래와 같음
- prophet은 주단위, 연단위 주기성을 잘 가지고 있음
- 점선은 예측한 것을 보여줌
- fig 6은 trend, weekly seasonality, and yearly seasonality components 을 나타냄
- The parameters tau and sigma in Listing 1 are controls for the amount of regularization
-
overfitting을 피하는데 regularization은 매우 중요
-
τ 를 바꿔서 주기성을 자주 반영
-
σ 를 바꿔서 주기성을 강하게 반영



3.5 Analyst-in-the-Loop Modeling
- 도메인 지식가는 통계적인 지식이 제한될 지라도 해당 분야 업무에 대한 도메인 지식이 있음
- prophet은 분석가가 모델을 적용할때 도메인 지식을 이용해서 적용해줘야할 파라미터가 있음
-
Capacities : 시장 규모와 어떤 것에 대한 용량 수준
-
ChangePoints : 상품이 바뀌거나 신제품이 출시되는 changepoints
-
Holiday and Seasonality : 성장에 영향을 미치는 특별한 휴일이나 이벤트 기간
-
Smoothing Parameter : 주기마다 변동을 줄 수준
- 위 조건들을 바꿔서 계속 Prophet을 실행하고, 시각화 툴을 가지고 확인
- 이를 통해 파라미터들을 조정하고 다시 플로팅하고 또 다시 재모델링 해보는 과정 반복될 수 있음
4 Automating Evaluation of Forecasts
- 자동으로 예측된 결과를 평가하는 메트릭에 대한 소개
4.1 Use of Baseline Forecasts
- 어떤 모델을 비교할떄 baseline과 비교하는 것이 매우 중요
- baseline 으로 last value, sample mean으로 매우 단순한 모델과 비교
4.2 Modeling Forecast Accuracy
- 예측은 특정 horizon H에 대해 이루어짐
-
전형적인 예를 들면 30, 90, 180, 365일과 같은 것으로 볼 수 있음
- 결과 평가 metric 은 전형적인 시간별 추정된 값과 실제값 사이의 MAE(mean absolute error) , MAPE(mean absolute percentage error) 임 → 해석상 MAPE 선호
- H에 따른 실증정확도는 아래 식과 같음

- 오차항은 아래와 같음

4.3 Simulated Historical Forecasts
- cross validation과 같은 방법을 사용하는 것은 매우 어려움 → 관측치들이 교환되지 않을 수 있기 때문
- 평가방법으로 simulated historical forecasts (SHFs)를 사용함
-
다양한 cutoff point에서 예측치 k 를 제공
- 아래 그림은 시계열 예측 알고리즘별 mape 를 H별로 비교한 그림
-
prophet의 errorr가 가장 낮은것을 볼 수 있음

4.4 Identifying Large Forecast Errors
- 분석가는 잘못된 예측 결과에 대해서도 확인하고, 이를 확인하고 수정할 필요가 있음
- 자동으로 잘못된 예측결과를 확인할 수 있게 해주는 것은 위와 같은 부분에서 분석가가 좀 더 효율적으로 일할 수 있게 도움
- SHFs can be used to identify likely problems with the forecasts
-
Baseline 모델과 비교하여 큰 에러가 있으면 trend, seasonality 등 수정
-
특정 일자에 예측률이 떨어진다면, 아웃라이어를 제거
-
특정 cutoff (연말 등) 에 예측률이 떨어진다면, changepoint를 추가
5 Conclusion
- prophet의 주된 목적은 다양한 기반지식을 가진 분석가가 보다 쉽게 시계열 예측을 활용하는 것
- 시계열의 복잡한 모델이 아닌 modular regression model을 이용하여 보다 직관적으로 이해할 수 있게 함
- 보다 쉽게 파라미터의 조정을 가능하게 했음
- 예측결과에 대한 정확성을 트래킹하는 시스템, 그리고 flagging 하는 것은 분석가가 분석을 보다 효율적으로 할 수 있게함
Reference
Prophet
- https://facebook.github.io/prophet/
- https://peerj.com/preprints/3190/
- Taylor, Sean J., and Benjamin Letham. "Forecasting at scale." The American Statistician 72.1 (2018): 37-45.