| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- GCP
- correlation
- chatGPT
- TensorFlow
- API Gateway
- 상관관계
- requests
- Retry
- gather_nd
- Airflow
- subdag
- top_k
- 유튜브 API
- integrated gradient
- youtube data
- login crawling
- hadoop
- 공분산
- Counterfactual Explanations
- grad-cam
- UDF
- GenericGBQException
- flask
- session 유지
- spark udf
- tensorflow text
- API
- airflow subdag
- XAI
- BigQuery
- Today
- Total
데이터과학 삼학년
큰 수의 법칙 (Law of Large Numbers (LoLN)), 중심극한의 정리 (Central Limit Theorem) 본문
큰 수의 법칙 (Law of Large Numbers (LoLN)), 중심극한의 정리 (Central Limit Theorem)
Dan-k 2020. 11. 17. 18:45큰 수의 법칙 vs 중심극한의 정리
> 표본의 크기를 크게 하냐?! --> 큰 수의 법칙
> 표본의 갯수를 많이 뽑냐?! --> 중심 극한의 정리
큰 수의 법칙 (Law of Large Numbers)
- 표본집단들의 평균과 분산에 대한 법칙
- 어떤 모집단에서 표본집단들을 추출할 때, 각 표본집단의 크기가 커지면 그 표본집단들의 평균은 모집단의 평균과 같아지고, 표본집단들의 분산은 0에 가까워 진다.
>> 한번 측정해서 평균을 구한 결과보다 여러번 시행해서 낸 평균값이 더 정확하다.

중심극한의 정리(Central limit theorem)
- 표본집단들의 평균이 갖는 분포에 대한 법칙
- 그 어떠한 모양의 임의의 분포에서 추출한 표본집단들의 평균(표본평균)의 분포는 정규분포를 이룬다.
(심지어 모집단이 정규분포를 따르지 않더라도. 단 각각의 표본의 크기가 적당히 커야한다. 30이상)

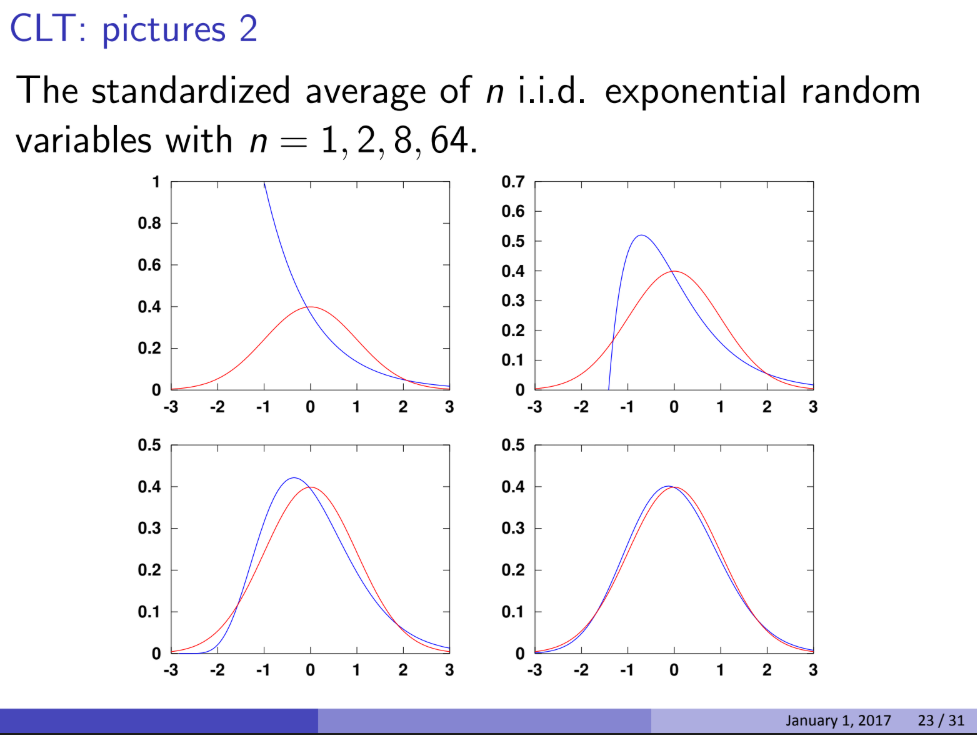
- 표본이 충분이 크다면(n>30), 표본들의 평균은 정규분포를 따른다.

- 중심극한의 정리가 중요한 이유
> 모집단의 분포에 상관없이, 모집단으로 부터 크기가 큰 표본들을 추출했을때, 그것이 정규분포를 따르기 때문에 통계적인 판단을 할 수 있음
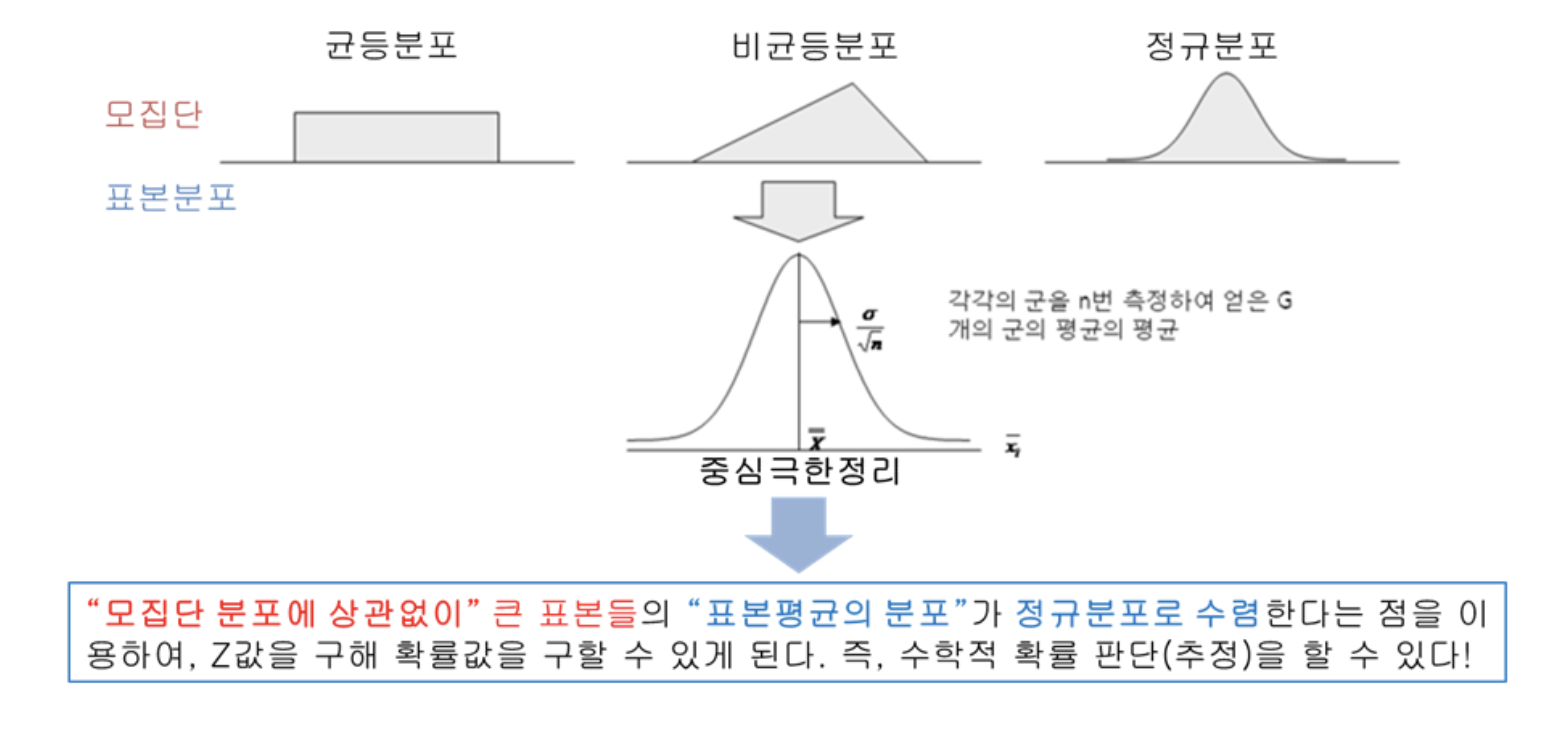
http://blog.daum.net/gongdjn/114
[11-4] 큰수의 법칙과 중심극한정리
※ 자료 출처 : Mathematical statistics with applications (K.M. Ramachandran, C. P. Tsokos 저) 앞에서 배웠던 체비세프의 정리, 큰수의 법칙, 중심극한 정리를 예를 들어 비교해보자. 1. 체비세프의 정리..
blog.daum.net
http://dermabae.tistory.com/146
중심극한정리
많은 통계모형들은 자료가 정규분포라는 가정에 기초하여 발달되었다. 그러므로 어떤 표본이 정규분포라는 가정을 할 수 있다면 다양한 분석법을 사용할 수 있어 통계적으로 매우 유리하다. 앞
dermabae.tistory.com
[개념 통계] 중심극한 정리는 무엇이고 왜 중요한가?
안녕하세요. 홍박사입니다. 정말 오랜만에 포스팅을 합니다. 바쁘다는 핑계로 계속 포스팅을 미뤄오다가 마음을 다잡고 짧은 호흡으로라도 포스팅을 하는 것이 좋을 것 같다는 생각이 들었습니
drhongdatanote.tistory.com
'Statistical Learning' 카테고리의 다른 글
| [기초통계] 공분산과 상관계수 (covarience, correlation) (0) | 2020.12.07 |
|---|---|
| [기초 통계] Q-Q Plot (feat. shapiro-test) (0) | 2020.11.28 |
| Outliers & leverage (1) | 2020.11.06 |
| [기초통계] 1종 오류와 2종 오류 (0) | 2020.11.05 |
| 다중 회귀 분석 vs 다항 회귀 분석 (Multiple VS Polynomial regression analysis) (0) | 2020.11.04 |




