| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- gather_nd
- GCP
- 상관관계
- BigQuery
- requests
- flask
- subdag
- 유튜브 API
- Airflow
- chatGPT
- correlation
- airflow subdag
- tensorflow text
- API
- 공분산
- TensorFlow
- GenericGBQException
- Counterfactual Explanations
- Retry
- grad-cam
- session 유지
- XAI
- UDF
- top_k
- API Gateway
- integrated gradient
- youtube data
- login crawling
- hadoop
- spark udf
- Today
- Total
데이터과학 삼학년
[유사도 분석] angular distance (vs cosine similarity) 본문
유사도 분석에서 흔히들 말하는 cosine similarity가 있다.
그러나 cosine similarity는 한계를 가지고 있어 이를 변형한
angular distance에 대해 소개하도록 하겠다.
cosine similarity 문제점
cosine similarity는 두 벡터간의 각도가 작으면 매우 비슷한 similarity를 갖는다는 것이다.
the problem with the cosine similarity is that small angles have very similar cosines. (In the diagram further below, compare the curves near the top edge.)
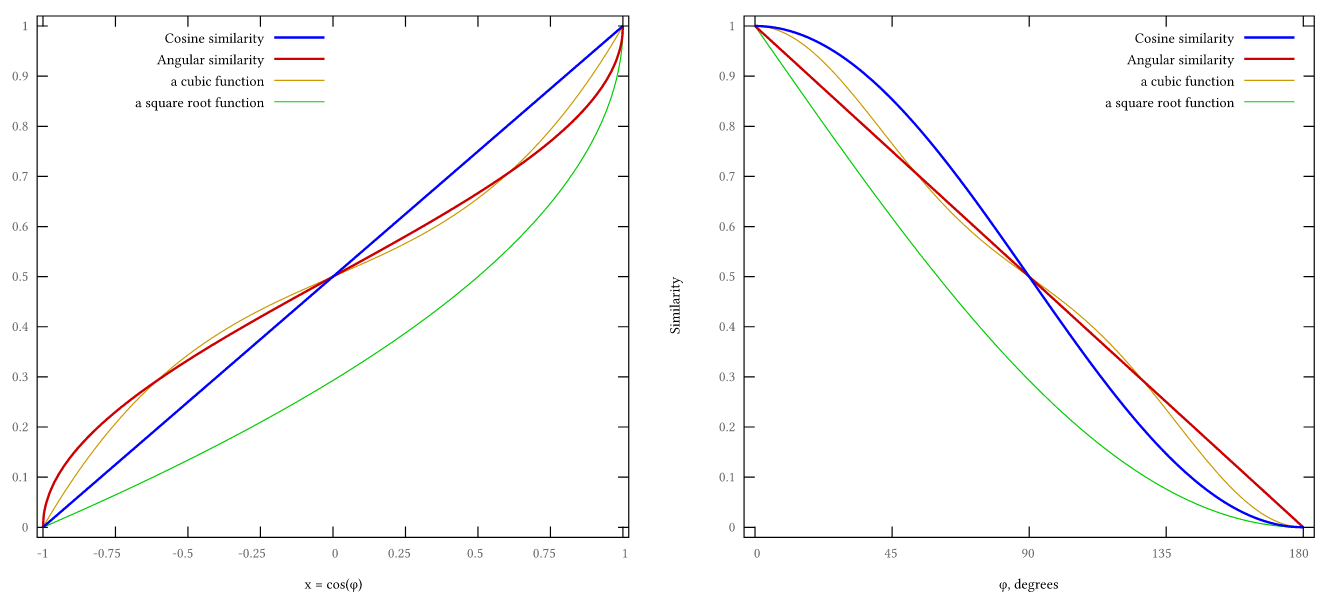
위 그래프에서 사용된 함수는 아래와 같다.
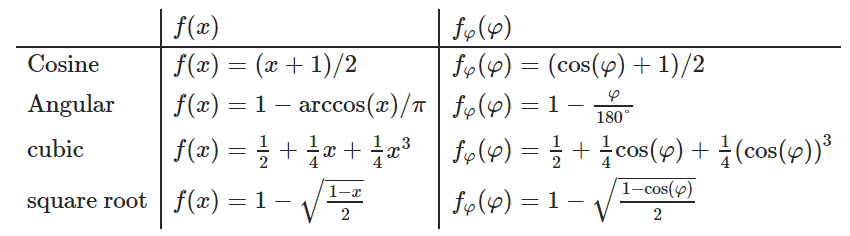
위 그래프의 왼쪽에서 보면 consine similarity는 각도차가 적을수록 그 값이 거의 비슷한 것을 알 수 있음
Picking f(x)=1−arccos(x)/π as the "similarity" mapping function was an easy, obvious choice by the authors of the referred to paper: it is easy to describe (35 or so words needed in the paper, including the footnote!), very intuitive, and according to the paper, sufficiently emphasizes non-"similarity" for vector pairs having a small angle, compared to the cosines of their angles.
사실 왼쪽 그래프를 보면 squere root를 이용한 함수가 각도가 적은 부분에 대해 더 큰 차이를 냄을 알 수 있어서 저 방법도 고려해 볼만 하다.
f(x)=1−{(1−x)/2}
https://math.stackexchange.com/questions/2874940/cosine-similarity-vs-angular-distance/2876675
Cosine similarity vs angular distance
While checking Google's Universal sentence encoder paper, I found that they mention that using a similarity based on angular distance performs better than raw cosine similarity. More specifically...
math.stackexchange.com
'Machine Learning' 카테고리의 다른 글
| GANs 간략한 소개 (0) | 2020.08.10 |
|---|---|
| CNN for sequence models (0) | 2020.08.10 |
| [TF 2.2] Text Vectorization Layer 적용된 모델의 예측 방법 (feat.GCP) (0) | 2020.07.27 |
| [TF 2.2] tf.keras.layers.experimental.preprocessing.TextVectorization 한계와 해결 방법 (0) | 2020.07.17 |
| Keras API 간단 정리 (From. Google Developers ) (0) | 2020.07.16 |



