| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- tensorflow text
- 상관관계
- gather_nd
- 유튜브 API
- Airflow
- flask
- correlation
- login crawling
- session 유지
- Retry
- hadoop
- grad-cam
- GCP
- API
- subdag
- airflow subdag
- XAI
- 공분산
- youtube data
- Counterfactual Explanations
- API Gateway
- TensorFlow
- BigQuery
- requests
- UDF
- GenericGBQException
- spark udf
- chatGPT
- integrated gradient
- top_k
- Today
- Total
데이터과학 삼학년
MAB(Multi-Armed Bandit), 톰슨 샘플링 본문
1. MAB란 무엇인가?
Multi-Armed Bandit(MAB) 문제는 여러 개의 슬롯 머신(팔을 당기는 밴딧) 중에서 어느 것을 선택해야 가장 높은 보상을 얻을 수 있는지 결정하는 문제입니다. 이 문제는 탐색(Exploration)과 활용(Exploitation) 사이의 균형을 잡는 것이 핵심입니다.

주요 구성 요소
- 팔(Arm): 선택 가능한 슬롯 머신 또는 행동.
- 보상(Reward): 선택한 팔에서 얻는 결과(예: 클릭, 구매 등).
- 목표: 보상의 합계를 최대화.
MAB 문제는 A/B 테스트, 광고 배치, 콘텐츠 추천 등 다양한 실생활 문제에 응용됩니다.
2. 탐색과 활용의 트레이드오프
MAB의 가장 큰 도전 과제는 탐색과 활용 사이의 트레이드오프를 해결하는 것입니다.
- 탐색(Exploration): 더 나은 팔을 찾기 위해 새로운 선택을 시도.
- 활용(Exploitation): 현재 가장 성과가 좋은 팔을 선택하여 보상을 극대화.
예시
만약 3개의 팔을 가진 슬롯 머신이 있다고 가정해봅시다. 각각의 팔은 서로 다른 확률로 보상을 제공합니다. 이 확률을 미리 알 수 없기 때문에 탐색과 활용을 통해 최적의 팔을 찾아야 합니다.
3. 톰슨 샘플링(Thompson Sampling)
개요
톰슨 샘플링은 확률론적 방법을 이용해 탐색과 활용을 균형 있게 수행하는 알고리즘입니다. 각 팔의 보상 분포를 추정하기 위해 베타 분포를 사용합니다.
동작 원리
- 각 팔에 대해 베타 분포를 초기화합니다.
- 베타 분포의 초기값은 (모두 동일한 사전 정보).
- 알파가 커질수록 오른쪽으로 봉우리가 이동!!!! -> 즉, 선택(성공)될 수록 선택될 확률이 높아지는 것!!
- 각 팔에서 샘플을 한 번씩 추출합니다.
- 가장 높은 샘플 값을 가진 팔을 선택합니다.
- 선택한 팔의 결과에 따라 베타 분포를 업데이트합니다.
- 성공(보상 획득):
- 실패(보상 미획득):
- 위 과정을 반복합니다.
4. 예제 코드
아래는 톰슨 샘플링을 구현한 Python 코드입니다:
import numpy as np
from scipy.stats import beta
import matplotlib.pyplot as plt
# 팔의 실제 보상 확률
true_conversion_rates = [0.1, 0.3, 0.5]
num_arms = len(true_conversion_rates)
# 각 팔의 베타 분포 파라미터 초기화
alpha = np.ones(num_arms)
beta_params = np.ones(num_arms)
# 시뮬레이션 설정
num_trials = 1000
rewards = np.zeros(num_trials)
for trial in range(num_trials):
# 1. 각 팔의 샘플링
sampled_theta = [np.random.beta(alpha[i], beta_params[i]) for i in range(num_arms)]
# 2. 가장 높은 샘플 값을 가진 팔 선택
chosen_arm = np.argmax(sampled_theta)
# 3. 선택된 팔에서 보상 관찰
reward = np.random.rand() < true_conversion_rates[chosen_arm]
# 4. 보상에 따라 베타 분포 업데이트
if reward:
alpha[chosen_arm] += 1
else:
beta_params[chosen_arm] += 1
# 보상 기록
rewards[trial] = reward
# 5. 주기적으로 베타 분포 시각화
if trial % 200 == 0 or trial == num_trials - 1:
x = np.linspace(0, 1, 1000)
plt.figure(figsize=(12, 6))
for i in range(num_arms):
plt.plot(x, beta.pdf(x, alpha[i], beta_params[i]), label=f"Arm {i+1}: Beta({alpha[i]}, {beta_params[i]})")
plt.title(f"Trial {trial+1}")
plt.legend()
plt.show()
print(f"총 보상: {rewards.sum()}")5. 결과 분석
위 코드는 다음을 보여줍니다:
- 초기에는 각 팔에 대해 고르게 탐색합니다.
- 시간이 지남에 따라 가장 보상이 높은 팔을 점점 더 자주 선택하게 됩니다.
- 각 팔의 베타 분포는 트라이얼이 진행됨에 따라 업데이트됩니다.
시각화
각 팔의 베타 분포를 시각화하면 탐색 및 활용 과정에서 팔들의 우선순위가 어떻게 변화하는지 확인할 수 있습니다.
처음에는 각 arm의 확률 분포를 기준으로 랜덤하게 선택했을때 선택되는 arm이 다를 수 있지만,
시도(exploration)가 반복됨에 따라 각 arm의 확률분포가 극단적으로 수렴하여 랜덤하게 선택되어도, 가장 우측에 봉우리가 만들어진 arm이 계속 선택될 것(exploitation)

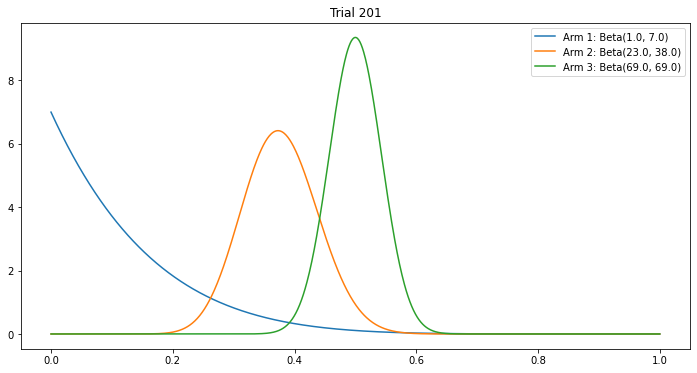
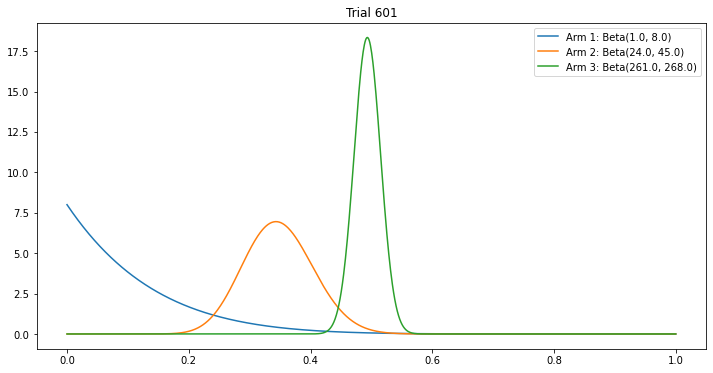

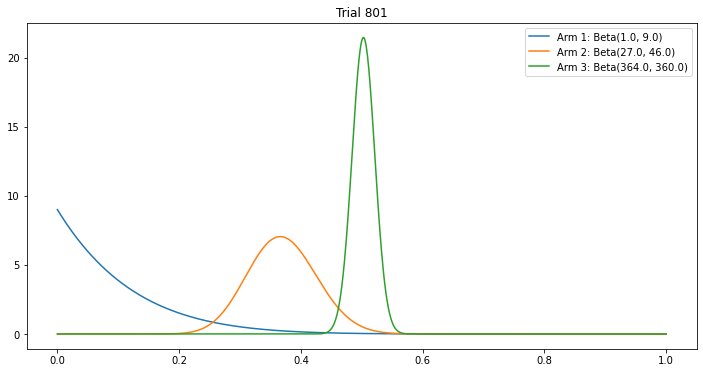
6. 결론
톰슨 샘플링은 간단하면서도 강력한 MAB 알고리즘입니다. 베타 분포를 활용해 확률론적으로 최적의 선택을 수행하며, 실생활의 다양한 문제에 적용 가능합니다.
MAB 알고리즘은 온라인 광고, 콘텐츠 추천, 의료 실험 등 다양한 분야에서 큰 가치를 제공합니다. 특히, 탐색과 활용의 균형을 자동으로 맞춘다는 점에서 실용성이 매우 높습니다.
import numpy as np
class ThompsonSampling:
def __init__(self, num_arms):
self.num_arms = num_arms
self.successes = np.ones(num_arms) # 각 팔의 성공 횟수 초기화
self.failures = np.ones(num_arms) # 각 팔의 실패 횟수 초기화
def select_arm(self):
# 각 팔에 대한 베타 분포에서 샘플링
samples = np.random.beta(self.successes, self.failures)
# 가장 높은 확률 값을 가진 팔 선택
return np.argmax(samples)
def update(self, chosen_arm, reward):
if reward:
self.successes[chosen_arm] += 1
else:
self.failures[chosen_arm] += 1
def run_experiment(num_arms, trials, data):
ts = ThompsonSampling(num_arms)
total_reward = 0
for _ in range(trials):
selected_arm = ts.select_arm()
reward = get_reward(selected_arm, data)
total_reward += reward
ts.update(selected_arm, reward)
return total_reward
# 예시 데이터
data = {0: 0.3, 1: 0.7, 2: 0.2} # 각 팔의 실제 보상 확률
num_arms = len(data)
trials = 1000
total_reward = run_experiment(num_arms, trials, data)
print("Total reward:", total_reward)참고자료
https://multithreaded.stitchfix.com/blog/2020/08/05/bandits/\
Multi-Armed Bandits and the Stitch Fix Experimentation Platform | Stitch Fix Technology – Multithreaded
We understand that there is a lot going on in the world right now. We’re continuing to publish blog posts in the hope they provide some intellectual stimulation and a sense of connection during these times. See the following for actions that we’re taki
multithreaded.stitchfix.com
'Recommendation System' 카테고리의 다른 글
| LLM을 활용한 추천 시스템 (0) | 2025.01.27 |
|---|---|
| Learning to Rank :: Pointwise, Pairwise, Listwise (2) | 2024.09.05 |
| 추천시스템 :: Retrieval, Ranking (1) | 2024.09.02 |
| 추천 메트릭 :: Precision@k, Recall@k, MAP, MRR, NDCG , AP, F1-Score, Coverage, Diversity, Novelty (0) | 2024.08.28 |
| 추천 Ranking 알고리즘 관련 metric :: NDCG (0) | 2024.08.23 |

