| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 상관관계
- tensorflow text
- session 유지
- API
- Retry
- youtube data
- XAI
- top_k
- Counterfactual Explanations
- integrated gradient
- requests
- Airflow
- API Gateway
- spark udf
- hadoop
- subdag
- GenericGBQException
- airflow subdag
- 공분산
- UDF
- 유튜브 API
- flask
- chatGPT
- gather_nd
- grad-cam
- BigQuery
- login crawling
- TensorFlow
- GCP
- correlation
- Today
- Total
데이터과학 삼학년
이중차분법 (Difference In Difference) 본문
이중차분법 (Difference In Difference)
- 원인과 결과간의 효과를 측정하기 위한 인과 추론 방법으로, 시계열적인 변화를 고려하여 효과 측정방법으로 이해됨
- 인과 추론에서는 실험군(Treated Group)과 대조군(Control Group)간의 차이가 있음을 인정하고 비교하는 방법으로, 비실험군이(unTreated Group)이 처치를 받지 않았다면 그 결과는 대조군(Control Group)의 결과(트렌드 변화)와 같다이다. → parallel trend assumption
- 이중차분법을 구하는 방법은 아주 간단함 : 실험군의 처치후 변화량에서 대조군의 트렌드 변화량을 빼주면 됨

- 평행 트렌드 가정(parallel trend assumption) 하에, "실험군이 처치를 받지 않았다면 나타났을 결과 변수의 트렌드 변화"는 "대조군의 결과 변수 트렌드 변화"가 동일할 것이기 때문입니다. 이를 추론하여 표시한 것이 빨간색 점선임
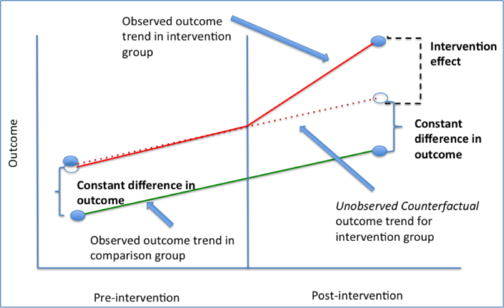

손호성,이재훈 (2018).
- 이렇게 이중으로 차분을 하면 두 집단 간의 특징 차이(종단면)를 제거하고, 시점에 따른 결과 변수의 변화(횡단면)가 얼마나 다르게 일어나는지 확인가능
Difference-in-Differences (이중차분법)
📚 Difference in Differences ✅ 기본 개념 DID는 특정 사건 전후로 실험집단과 통제집단의 차이를 비교해보는데 쓰인다(World Bank. 2010) 실험집단과 동질적인 통제집단을 설정하여 전후관계를 비교함
yeong-jin-data-blog.tistory.com
https://everyday-tech.tistory.com/entry/%EC%9D%B4%EC%A4%91%EC%B0%A8%EB%B6%84%EB%B2%95DID
이중차분법(DID)
본 포스팅은 이중 차분법에 대해 공부한 내용을 정리한 글입니다 :) 참고 서적 : Joshua D. Angrist, Jorn-Steffen Pischke. (2018). 고수들의 계량경제학. 시그마프레스. p.178 ~ p.190 이중 차분법 컨셉 이중..
everyday-tech.tistory.com
'Statistical Learning' 카테고리의 다른 글
| Simpson's paradox (심슨의 역설) (1) | 2023.03.04 |
|---|---|
| 통계적 편향 (통계로 거짓말하기) (0) | 2022.09.05 |
| 분산분석 (ANOVA : ANalysis Of VAriance) (0) | 2022.07.14 |
| Chi-Square Distribution (카이제곱분포) (1) | 2022.06.03 |
| 선형 회귀 분석의 가정 (1) | 2022.05.23 |


