SVD (Singular Value Decomposition) 특이값 분해

특이값 분해(Singular Value Decomposition, SVD)는 임의의 m×n차원의 행렬 A에 대하여 다음과 같이 행렬을 분해할 수 있다는 ‘행렬 분해(decomposition)’ 방법

 

 임의의 m×n차원의 행렬 A에 대하여 다음과 같이 행렬을 분해할 수 있다는 ‘행렬 분해(decomposition)’ 방법



여기서 Σ 는 특이값을 나타내는 행렬이다.

 

SVD 의 활용은 Truncated SVD 로 분해한 행렬을 토대로 얼마 차원을 줄일지 t를 정한 이후

t만큼의 정보를 남기고 다시 곱해 A' 행렬을 만들어 내는 것이다.

 

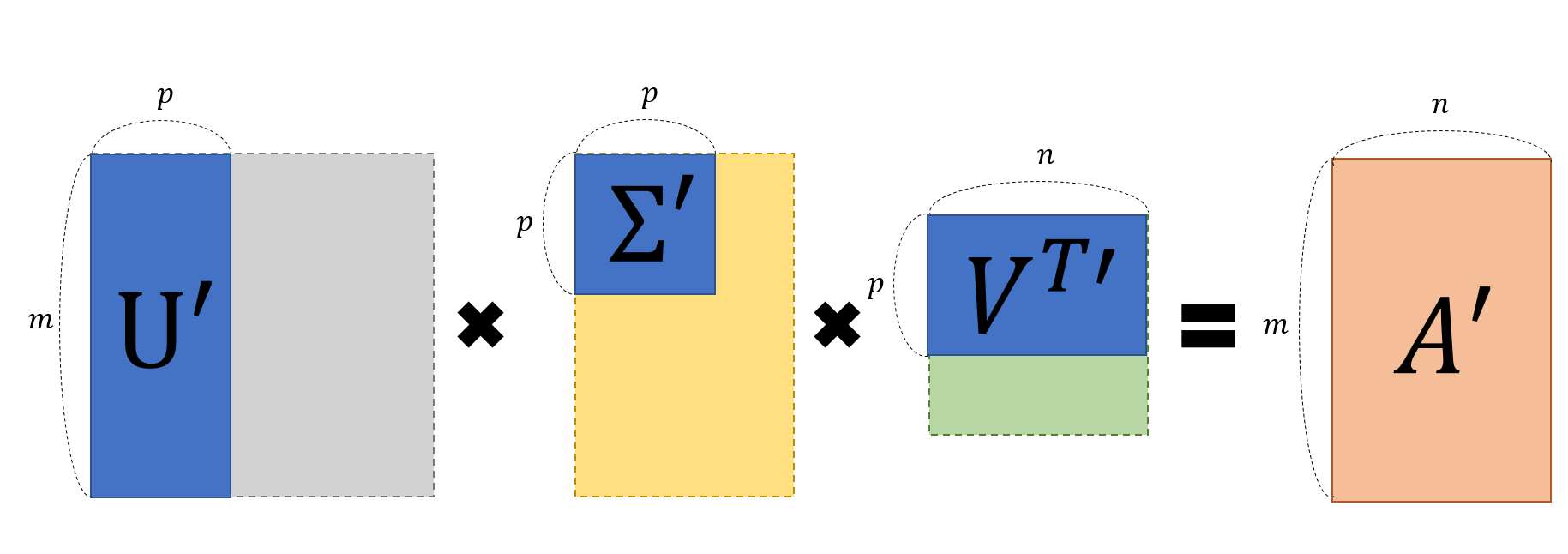
여기서 A' 행렬은 A행렬의 특징을 모아놓은 행렬로 볼 수 있다.

 

이런 방법을 활용한 것 중 하나가 LSA (Latent Simentic Analysis)이다.

 

 

numpy 를 이용해 간단히 SVD를 실습할 수 있다.

 

import numpy as np

a = np.random.randn(9, 6) + 1j*np.random.randn(9, 6)
b = np.random.randn(2, 7, 8, 3) + 1j*np.random.randn(2, 7, 8, 3)


u, s, vh = np.linalg.svd(a, full_matrices=True)
u.shape, s.shape, vh.shape
((9, 9), (6,), (6, 6))
np.allclose(a, np.dot(u[:, :6] * s, vh))
True
smat = np.zeros((9, 6), dtype=complex)
smat[:6, :6] = np.diag(s)
np.allclose(a, np.dot(u, np.dot(smat, vh)))
True


u, s, vh = np.linalg.svd(a, full_matrices=False)
u.shape, s.shape, vh.shape
((9, 6), (6,), (6, 6))
np.allclose(a, np.dot(u * s, vh))
True
smat = np.diag(s)
np.allclose(a, np.dot(u, np.dot(smat, vh)))
True


u, s, vh = np.linalg.svd(b, full_matrices=True)
u.shape, s.shape, vh.shape
((2, 7, 8, 8), (2, 7, 3), (2, 7, 3, 3))
np.allclose(b, np.matmul(u[..., :3] * s[..., None, :], vh))
True
np.allclose(b, np.matmul(u[..., :3], s[..., None] * vh))
True


u, s, vh = np.linalg.svd(b, full_matrices=False)
u.shape, s.shape, vh.shape
((2, 7, 8, 3), (2, 7, 3), (2, 7, 3, 3))
np.allclose(b, np.matmul(u * s[..., None, :], vh))
True
np.allclose(b, np.matmul(u, s[..., None] * vh))
True